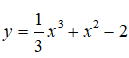
Câu 6: Cho hàm số
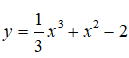
Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ là nghiệm của phương trình y” = 0 là
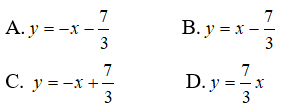
Câu 7: Cho hàm số
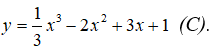
Tìm phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến đó song song với đường thẳng y = 3x -1
A. y = 3x + 1 B. y = 3x – 29/3 C. 3x + 20 D. Cả A và B đúng
Câu 8: Gọi M, N là giao điểm của
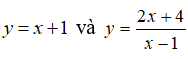
Khi đó hoành độ trung điểm của I của đoạn thẳng MN bằng
A. 2 B.1 C. 0 D. -1
Câu 9: Tìm m để phương trình x3 + 3x2 = m có ba nghiệm phân biệt
A. m > 4 B. m < 0 C. 0 ≤ m ≤ 4 D. 0 < m < 4
Hướng dẫn giải và Đáp án
| 6-A | 7-D |
Câu 6:
Ta có
y’ = x2 + 2x; y” = 2x + 2 => y” = 0 <=> x = -1 => -4/3, y'(-1) = -1
Phương trình tiếp tuyến của đồ thị hàm số tại điểm x = -1 là:
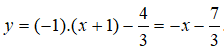
Chọn đáp án A.
Câu 7:
Ta có y’ = x2 – 4x + 3. Tiếp tuyến của đồ thị (C) song song với đường thẳng y = 3x – 1 nên hệ số góc của tiếp tuyến là k = 3.
Xét y’ = 3 <=> x2 – 4x = 0
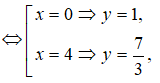
Phương trình tiếp tuyến của đồ thị tại A(0;1) có hệ số góc k = 3 là y = 3x + 1
Phương trình tiếp tuyến của đồ thị tại B(4; 7/3) có hệ số góc k = 3 là y = 3x – 29/3 .
Chọn đáp án D.
Câu 8:
Xét phương trình hoành độ giao điểm
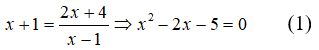
Giao điểm của hai đồ thị hàm số là M(x1; y1), N(x2; y2) với x1, x2 là nghiệm phương trình (1). Do đó
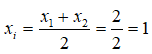
Chọn đáp án B.
Câu 9:
Xét hàm số
y = f(x) = x3 + 3x2 (C)
Đồ thị hàm số có dạng như hình bên.
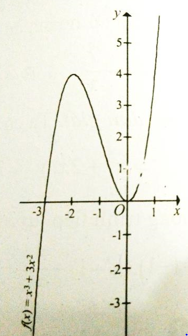
x3 + 3x2 = m có ba nghiệm phân biệt
<=> Đường thẳng y = m cắt đồ thị (C) tại ba điểm phân biệt <=> 0 < m < 4
Chọn đáp án D.