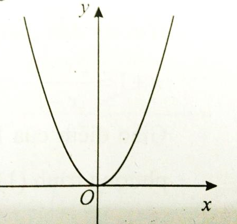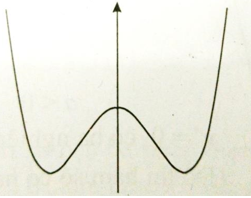
Câu 1: Đường cong trong hình dưới đây là đồ thị của một hàm số trong 4 hàm số được liệt kê ở 4 phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?

A. y = x4 + 3x2 – 2
B. y = x3 – 2x2 + 1
C. y = -4x4 + x2 + 4
D. y = x4 – 2x2 + 3
Câu 2: Đồ thị trong hình dưới đây là đồ thị của đồ thị hàm số nào?
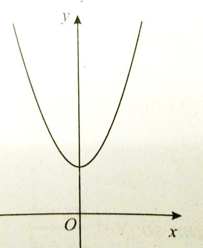
A. y = x2 – 2x + 1
B. y = x3 + 4x2 – 2x + 5
C. y = x4 + x2 + 1
D. y = x4 – 3x2 + 5
Câu 3: Tâm đối xứng của đồ thị hàm số y = -x3 – 3x2 + 1 là:
A. (-1; -1) B. (-2; -3) C. (0; 1) D. Không có đáp án
Câu 4: Trong các mệnh đề sau, mệnh đề nào đúng?
A. I(1; 0) là tâm đối xứng của
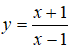
B. I(1; 0) là tâm đối xứng của y = -x3 + 3x2 – 2
C. I(1; 0) là điểm thuộc đồ thị
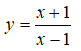
D. I(1; 0) là giao điểm của y = x3 – 3x2 – 2 với trục hoành.
Câu 5: Tìm m để bất phương trình x4 + 2x2 ≥ m luôn đúng.
A. m = 0 B. m < 0
C. m ≤ 0 D. Không có đáp án
Hướng dẫn giải và Đáp án
| 1-D | 2-C | 3-A | 4-B | 5-C |
Câu 1:
Theo Chú ý ở mục 2, đồ thị ứng với hàm bậc bốn trùng phương có a > 0 và a, b, trái dấu.
Chọn đáp án D.
Câu 2:
Theo Chú ý ở mục 2, đồ thị ứng với hàm bậc bốn trùng phương có a > 0 và a, b, cùng dấu hoặc hàm số bậc hai với a > 0. Tuy nhiên đỉnh của parabol của đồ thị hàm số y = -x3 – 3x2 + 1 là I(1; 0) nằm trên trục hoành.
Chọn đáp án C.
Câu 3:
y’ = -3x2 – 6x; y” = -6x – 6; y” = 0 => x = -1
Vậy điểm U(-1; -1) là tâm đối xứng của đồ thị (theo chú ý ở mục 1).
Chọn đáp án A.
Câu 4:
A. Tâm đối xứng của
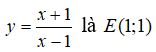
C. Điểm I(1; 0) không thuộc đồ thị
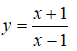
D. Điểm I(1; 0) không thuộc đồ thị y = x3 – 3x2 – 2 nên không phải là giao điểm của y = x3 – 3x2 – 2 với trục hoành.
Chọn đáp án B.
Câu 5:
Xét hàm y = x4 + 2x2 ≤ m có a = 1 > 0; b = 2 > 0 => a, b cùng dấu.
Đồ thị có dạng như hình bên.
Từ đồ thị hàm số ta suy ra m ≤ 0 . Chọn đáp án C.