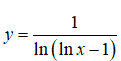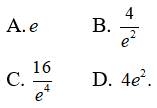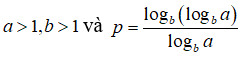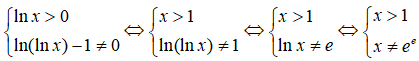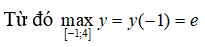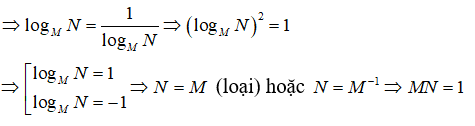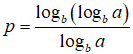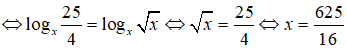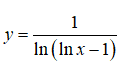
Câu 20: Tìm miền xác định của hàm số

A. D = (1; +∞)\{e^e}   B. D = (0; +∞)\{e}

C. D = (e^e; +∞)   D. D = (1; +∞)\{e}

Câu 21: Ngày 15 tháng 2 năm 2010 ông A gửi vào ngân hàng 500 triệu đồng với hình thức lãi kép và lãi suất 10,3% một năm. Tại thời điểm đó ông A dự tính sẽ rút hết tiền ra vào 15 tháng 2 năm 2013. Nếu trong khoảng thời gian đó lãi suất không thay đổi thì số tiền mà ông A rút được là bao nhiêu? Làm tròn kết quả đến hàng nghìn.

A. 608305000 đồng.     B. 665500000 đồng.

C. 670960000 đồng.    D. 740069000 đồng.

Câu 22: Tìm giá trị lớn nhất của hàm số y = x²e^-x trên đoạn [-1; 4]

Câu 23: Tìm tập nghiệm của phương trình log(x + 3) + log(x – 1) = log(x² – 2x -3)

A. ∅    B. {0}     C. R    D. (1; +∞)

Câu 24: Biết rằng log_MN = log_NM và N ≠ . Tính giá trị của MN.

A. -1    B. 1    C. 2   D. 10

Câu 25: Biết:

Khi đó a^p bằng

A. log_ab   B. a^log_ba   C. log_ba   D. b

Câu 26: Giả sử x là nghiệm của phương trình log_x25 – log_x4 = log_x√x.

Hướng dẫn giải và Đáp án

20-A

21-C

22-A

23-A

24-B

25-C

26-D

Câu 20:

Điều kiện

Vậy miền xác định của hàm số là D = (1; +∞)\{e^e}

Câu 21:

Số tiền ông A rút được : 500000000.(1 + 0,103)³ = 670959863 ≈ 970960000 (đồng)

Câu 22:

y’ = 2xe^-x – x²e^-x = xe^-x(2 – x); y’ = 0 <=> x = 0 hoặc x = 2

y(-1) = e, y(0) = 0, y(2) = 4/e², y(4) = 16/e⁴

Câu 23:

Điều kiện x > 3. Khi đó: log(x + 3) + log(x – 1) = log(x² – 2x – 3)

<=> log[(x + 3)(x – 1)] = log(x² – 2x – 3) <=> x² + 2x – 3 = x² – 2x + 3

<=> 4x = 0 <=> x = 0 (loại).

Vậy phương trình vô nghiệm

Câu 24:

log_MN = log_NM

Câu 25:

plog_ba = log_b(log_ba) => log_ba^p = log_b(log_ba)

=> a^p = log_ba

Câu 26:

Điều kiện 9 < x ≠ 1

log_x25 – log_x4 = log_x√x

Comments

comments