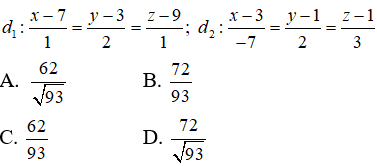
Câu 15: Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là x + y – 2z = 0; 2x + (m2 – m)y – 4z + 2m2 – 2m – 4 = 0, trong đó m là tham số. Tìm m để hai mặt phẳng (P) và (Q) song song
A. m=1 hoặc m=-2 C. m=-2
B. m=1 D. Không có m thỏa mãn bài toán
Câu 16: Trong không gian Oxyz, tính khoảng cách giữa hai đường thẳng:
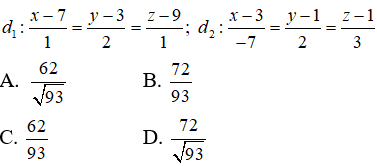
Câu 17: Tìm tất cả các giá trị của a để hai đường thẳng sau cắt nhau: d1: x = 1 + at, y = t, z = -1 + 2t, d2: x = 1 + t’, y = 2 – 2t’, z = 3 + t’
A. a > 0 B. a ≠ 4/3 C. a = 0 D. a ≠ 0
Câu 18: Trong không gian Oxyz, cho mặt cầu (S): (x + 1)2 + (y – 1)2 + (z – 1)2 = 4 và mặt phẳng (P): 3x – 4y – 4 = 0 . Có bao nhiêu đường thẳng d nằm trong mặt phẳng (P), đi qua điểm M(0;-1;2) và tiếp xúc với mặt cầu (S)
A. 0 B. 1 C. 2 D. Vô số
Câu 19: Trong không gian Oxyz, cho bốn điểm A(3;1;-1), B(1;1;1), C(2;1;0), D(-3;5;1). Có bao nhiêu mặt phẳng đồng thời cách đều cả bốn điểm A, B, C, D?
A. 0 B. 4 C. 7 D. Vô số
Câu 20: Cho các số a, b, c, m, n, p thay đổi nhưng luôn thỏa mãn các điều kiện: a2 + b2 + c2 + 4a – 2b – 4c ≤ 0 và 2m + 2n – p – 11 = 0. Tìm giá trị nhỏ nhất của biểu thức: P = (a – m)2 + (b – n)2 + (c – p)2
A. 0 B. 4 C. 2 D. 9
Hướng dẫn giải và Đáp án
| 15-D | 16-A | 17-C | 18-A | 19-D | 20-B |