Bài 1 (trang 120 SGK Hình học 11): Nhắc lại định nghĩa vectơ không gian.
Cho hình lăng trụ tam giác ABC.A’B’C’. Hãy kể tên những vectơ bằng vectơ có điểm đầu và điểm cuối là đỉnh của hình lăng trụ.
Lời giải:
Vectơ trong không gian là một đoạn thẳng có định hướng, tức là một đoạn thẳng đã được chỉ rõ điểm đầu và điểm cuối.
Vì các cạnh bên của hình lăng trụ là các đoạn thẳng song song và bằng nhau nên các vectơ bằng vectơ và có điểm đầu và điểm cuối là đỉnh của hình lăng trụ là: các vector BB’, CC’, DD’.
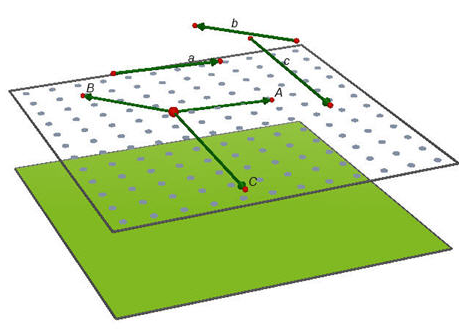
Bài 2 (trang 120 SGK Hình học 11): Trong không gian cho ba vectơ a , b và c đều khác vectơ 0 . Khi nào ba véc tơ đó đồng phẳng?
Lời giải:

Thỏa mãn :
– Giá của 3 vector đều song song với mặt phẳng (P) nên chúng đồng phẳng
– Khi ba vectơ có giá của chúng cùng song song với một mặt phẳng
Bài 3 (trang 120 SGK Hình học 11): Trong không gian hai đường thẳng không cắt nhau có thể vuông góc với nhau không? Giả sử hai đường thẳng a và b lần lượt có vectơ chỉ phương là vector u và vector v . Khi nào ta có kết luận a và b vuông góc với nhau?
Lời giải:
Trong không gian, hai đường thẳng vuông góc với nhau không nhất thiết phải cắt nhau vì vậy hai đường thẳng không cắt nhau vẫn có thể vuông góc với nhau.
Đường thẳng a có vectơ chỉ phương u→
Đường thẳng b có vectơ chỉ phương v→
a vuông góc với b khi và chỉ khi tích vô hướng của hai vectơ và bằng không. a ⊥ b ⇔u→ .v→ = 0.
Bài 4 (trang 120 SGK Hình học 11): Muốn chứng minh đường thẳng a vuông góc với mặt phẳng (α) có cần chứng minh a vuông góc với mọi đường thẳng của (α) hay không?
Lời giải:
Không cần chứng minh a vuông góc với mọi đường thẳng của mặt phẳng.
Ta có thể chọn một trong số những cách sau để chứng minh đường thẳng vuông góc với mặt phẳng
– Cách 1 : Chứng minh đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng
– Cách 2 : Sử dụng định lí : “Nếu hai mặt phẳng vuông góc với nhau thì bất kì đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến thì cũng vuông góc với mặt phẳng kia”.
– Cách 3 : Sử dụng định lí : ” Nếu hai mặt phẳng phân biệt cùng vuông góc với mặt phẳng thứ 3 thì giao tuyến của chúng cũng sẽ vuông góc với mặt phẳng đó”
Bài 5 (trang 120 SGK Hình học 11): Nhắc lại nội dung định lí ba đường thẳng vuông góc
Lời giải:
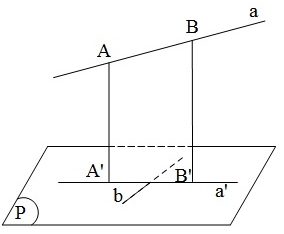
Cho đường thẳng a không vuông góc với mặt phẳng (P) và đường thẳng b nằm trong (P) . Khi đó, điều kiện cần và đủ để b vuông góc với a là b vuông góc với hình chiếu a’ của a trên (P).
Bài 6 (trang 120 SGK Hình học 11): Nhắc lại định nghĩa:
a) Góc giữa đường thẳng và mặt phẳng.
b) Góc giữa hai mặt phẳng.
Lời giải:
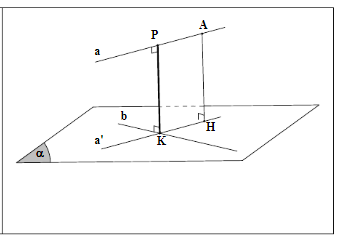
a) Định nghĩa: Góc giữa đường thẳng và mặt phẳng.
Cho đường thẳng d cắt mặt phẳng (α) tại điểm O và d không vuông góc với (α). Góc giữa đường thẳng d và mặt phẳng (α) là góc tạo bởi đường thẳng d và hình chiếu vuông góc góc d‘ của d trên mặt phẳng (α), kí hiệu góc (d,α).
– Nếu d vuông góc góc với (α) ta qui ước góc (d,α) = 90o.
– Nếu d // (α) hay d nằm trong (α) ta quy ước góc (d,α) = 90o.
b) Định nghĩa: Góc giữa hai mặt phẳng
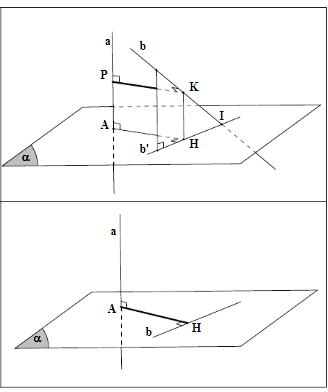
Giả sử hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến c. Từ điểm I bất kì trên c ta dựng trong (α) đường thẳng a vuông góc với c và dựng trong (β) đường thẳng b vuông góc với c. Ta gọi góc giữa hai đường a và b là góc giữa hai mặt phẳng (α) và (β). Như vậy góc giữa hai mặt phẳng (α) và (β) luôn có số đo bé hơn hoặc bằng 90o.
*Nếu hai mặt phẳng song song hoặc trùng với nhau thì ta nói rằng góc giữa hai mặt phẳng đó bằng 0o. Góc giữa hai mặt phẳng (α) và (β) được kí hiệu là (α, β), ta có 0o ≤ (α, β) ≤ 90o.
Bài 7 (trang 120 SGK Câu hỏi Hình học 11): Muốn chứng minh mặt phẳng (α) vuông góc với mặt phẳng (β) ta có thể ?
Lời giải:
Chứng minh (α) chứa một đường thẳng vuông góc với (β) hoặc (β) chứa một đường thẳng vuông góc với (α).
![]()
Hoặc chứng minh góc giữa (α) và (β) bằng 90o.
Bài 8 (trang 120 SGK Hình học 11): Hãy nêu cách tính khoảng cách :
a) Từ một điểm đến một đường thẳng ;
b) Từ đường thẳng a đến mặt phẳng (α) song song với a ;
c) Giữa hai mặt phẳng song song.
Lời giải:
a) Để tính khoảng cách từ điểm O đến đường thẳng Δ không đi qua O, ta xác định mặt phẳng (O; Δ) và trong mặt phẳng này kẻ OH ⊥ Δ. Độ dài OH chính là khoảng cách từ O đến Δ.
b) Để tính khoảng cách giữa đường thẳng a và mp(P) song song với (P), ta lấy một điểm M bất kì thuộc đường thẳng a. Khoảng cách MN từ điểm M đến mp(P) chính là khoảng cách giữa đường thẳng và mp(P) song song với a.
c) Để tính khoảng cách giữa hai mp(P) và (P‘) song song với nhau, ta lấy một điểm M thuộc (P) và tìm khoảng cách MH từ điểm M đến mp(P‘).
Bài 9 (trang 120 SGK Hình học 11): Cho a và b là hai đường thẳng chéo nhau. Có thể tính khoảng cách giữa hai đường thẳng chéo nhau này bằng những cách nào?
Lời giải:
Có 2 cách để tính khoảng cách giữa hai đường thẳng chéo nhau


Bài 10 (trang 120 SGK Hình học 11): Chứng minh rằng tập hợp các điểm cách đều ba đỉnh của một tam giác ABC là đường vuông góc với mặt phẳng (ABC) và đi qua tâm đường tròn ngoại tiếp tam giác ABC.
Lời giải:
Lấy một điểm M bất kì trong không gian sao cho MA = MB = MC. Từ M kẻ MO vuông góc với mp(ABC). Các tam giác vuông MOA, MOB, MOC bằng nhau, cho ta OA = OB = OC.
– Suy ra O là tâm đường tròn ngoại tiếp tam giác ABC. Vậy các điểm M cách đều ba đỉnh của tam giác ABC nằm trên đường thẳng d đi qua tâm O của đường tròn ngoại tiếp tam giác ABC và vuông góc với mp(ABC). Ngược lại, lấy một điểm M‘ ∈ d, nối M‘A, M‘B, M‘C.
– Do M‘O chung và OA = OB = OC nên các tam giác vuông M‘OA, M‘OB, M‘OC bằng nhau, cho ta M‘A = M‘B = M‘C.
– Tức là điểm M‘ cách đều ba đỉnh A, B, C của tam giác ABC.
– Kết luận : Tập hợp các điểm cách đều ba đỉnh của tam giác ABC là đường thẳng vuông góc với mp(ABC) và đi qua tâm của đường tròn ngoại tam giác ABC.