Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 32: Hãy nêu một ví dụ cụ thể về hàm số.

Lời giải

Sự phụ thuộc về quãng đường đi được của 1 xe khách với vận tốc và thời gian.

Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 33: Hãy chỉ ra các giá trị của hàm số trên tại x = 2001; 2004; 1999

Lời giải

x = 2001 ⇒ y = 375

x = 2004 ⇒ y = 564

x = 1999 ⇒ y = 339

Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 33: Hãy chỉ ra các giá trị của mỗi hàm số trên tại các giá trị x ∈ D

D = { 1995; 1996; 1997; 1998; 1999; 2000; 2001}

Lời giải

Hàm số: Tổng số công trình tham dự giải thưởng

x	1995	1996	1997	1998	1999	2000	2001
y	39	43	56	78	108	116	141

Hàm số: Tổng số công trình đạt giải thưởng

x	1995	1996	1997	1998	1999	2000	2001
y	10	17	23	28	29	35	43

Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 33: Hãy kể các hàm số đã học ở Trung học cơ sở

Lời giải

Các hàm số đã học là; hàm số bậc nhất y = ax + b; hàm số y = ax²

Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 34: Tìm tập xác định của các hàm số sau

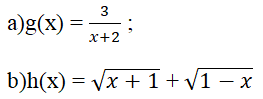
Lời giải

a) Biểu thức g(x) = 3/(x + 2) xác định khi x + 2 ≠ 0 ⇔ x ≠ -2

TXĐ của hàm số là D = R\{-2}

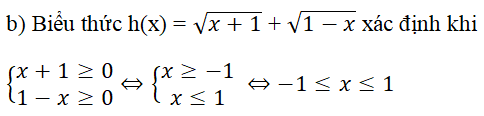
TXĐ của hàm số là D = [-1;1]

Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 34: Tính giá trị của hàm số ở chú ý trên tại x = -2 và x = 5.

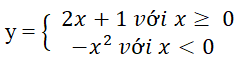
Lời giải

x = -2 ⇒ y = -(-2)² = -4

x = 5 ⇒ y = 2.5 + 1 = 11

Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 35: Dựa vào đồ thị của hai hàm số đã cho trong hình 14

y = f(x) = x + 1 và y = g(x) = 1/2 x²

Hãy:

a) Tính f(-2), f(-1), f(0), f(2), g(-1), g(-2), g(0);

b) Tìm x, sao cho f(x) = 2;

Tìm x, sao cho g(x) = 2;

Lời giải

a) f(-2) = -1; f(-1) = 0; f(0) = 1; f(2) = 3

g(-1) = 0,5; g(-2) = 2; g(0) = 0

b) f(x) = 2 ⇒ x = 1

g(x) = 2 ⇒ x = 2 hoặc x = -2

Trả lời câu hỏi Toán 10 Đại số Bài 1 trang 38: Xét tính chẵn lẻ của các hàm số

a)y = 3x² – 2; b) y = 1/x; c) y = √x

Lời giải

a) y = f(x) = 3x² – 2

TXĐ:D = R ⇒ x ∈ D thì-x ∈ D

Ta có: f(-x) = 3(-x)² – 2 = 3x² – 2 = f(x)

Vậy hàm số y = f(x) = 3x² – 2 là hàm số chẵn

b) y = f(x) = 1/x

TXĐ: D = R \{0} ⇒ x ∈ D thì-x ∈ D

f(-x) = 1/(-x) = -1/x = -f(x)

Vậy y = f(x) = 1/x là hàm số lẻ.

c) y = √x

TXĐ: D = [0; +∞) ⇒ x ∈ D thì -x ∉ D

Vậy hàm số trên không là hàm số chẵn cũng không là hàm số lẻ.

Bài 1 (trang 38 SGK Đại số 10): Tìm tập xác định của hàm số:

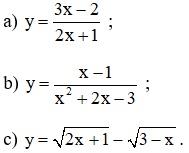
Lời giải:

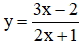
a) có nghĩa khi 2x + 1 ≠ 0 ⇔ x ⇔ –1/2.

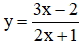
Vậy tập xác định của hàm là D = R \ {-1/2}.

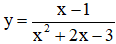
b) xác định khi x² + 2x – 3 ≠ 0.

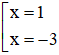
Giải phương trình x² + 2x – 3 = 0 ⇔ (x-1)(x+3) = 0 ⇔

Do đó x² + 2x – 3 ≠ 0 khi x ≠ 1 và x ≠ -3.

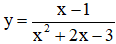
Vậy tập xác định của hàm số là D = R \ {1;-3}

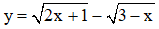
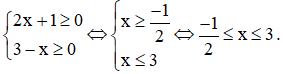
c) xác định khi

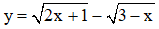
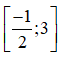
Vậy tập xác định của hàm số là

Kiến thức áp dụng

+ Hàm phân thức xác định nếu mẫu số khác 0.

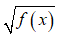
+ Hàm xác định khi f(x) ≥ 0.

Bài 2 (trang 38 SGK Đại số 10): Cho hàm số

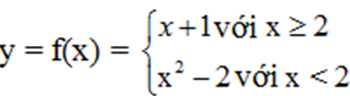
Tính giá trị của hàm số đó tại x = 3; x = -1; x = 2.

Lời giải:

– Ta có : x = 3 > 2 nên f(3) = 3 + 1 = 4.

– Ta có : x = -1 < 2 nên f(–1) = (-1)² – 2 = –1.

– Ta có : x = 2 nên f(2) = 2 + 1 = 3.

Kiến thức áp dụng

+ Một hàm số có thể được cho bởi hai, ba hoặc nhiều công thức.

Bài 3 (trang 39 SGK Đại số 10): Cho hàm số y = 3x² – 2x + 1. Các điểm sau có thuộc đồ thị của hàm số không ?

a) M(-1 ; 6)

b) N(1 ; 1)

c) P(0 ; 1)

Lời giải:

Tập xác định của hàm số y = f(x) = 3x² – 2x + 1 là D = R

a) Tại x = –1 thì y = 3.( –1)² – 2. (–1) + 1 = 3 + 2 + 1 = 6.

Vậy điểm M(–1; 6) thuộc đồ thị hàm số y = 3x² – 2x + 1.

b) Tại x = 1 thì y = 3.1² – 2.1 + 1 = 3 – 2 + 1 = 2 ≠ 1.

Vậy N(1; 1) không thuộc đồ thị hàm số.

c) Tại x = 0 thì y = 3.0² – 2.0 + 1 = 1.

Vậy điểm P(0 ; 1) thuộc đồ thị hàm số.

Kiến thức áp dụng

Điểm A(x₀;y₀) thuộc đồ thị hàm số y = f(x) nếu y₀ = f(x₀).

(Kiến thức lớp 7).

Bài 4 (trang 39 SGK Đại số 10): Xét tính chẵn lẻ của các hàm số sau:

a) y = |x|;

b) y = (x + 2)²;

c) y = x³ + x;

d) y = x² + x + 1.

Lời giải:

a) Đặt y = f(x) = |x|.

+ Tập xác định D = R nên với ∀ x ∈ D thì –x ∈ D.

+ f(–x) = |–x| = |x| = f(x).

Vậy hàm số y = |x| là hàm số chẵn.

b) Đặt y = f(x) = (x + 2)².

+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.

+ f(–x) = (–x + 2)² = (x – 2)² ≠ (x + 2)² = f(x)

+ f(–x) = (–x + 2)² = (x – 2)² ≠ – (x + 2)² = –f(x).

Vậy hàm số y = (x + 2)² không chẵn, không lẻ.

c) Đặt y = f(x) = x³ + x.

+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.

+ f(–x) = (–x)³ + (–x) = –x³ – x = – (x³ + x) = –f(x)

Vậy y = x³ + x là một hàm số lẻ.

d) Đặt y = f(x) = x² + x + 1.

+ TXĐ: D = R nên với ∀x ∈ D thì –x ∈ D.

+ f(–x) = (–x)² + (–x) + 1 = x² – x + 1 ≠ x² + x + 1 = f(x)

+ f(–x) = (–x)² + (–x) + 1 = x² – x + 1 ≠ –(x² + x + 1) = –f(x)

Vậy hàm số y = x² + x + 1 không chẵn, không lẻ.

Kiến thức áp dụng

Cho hàm số y = f(x) với tập xác định D:

+ f(x) là hàm số chẵn nếu: với ∀x ∈ D thì –x ∈ D và f(–x) = f(x).

+ f(x) là hàm số lẻ nếu: với ∀x ∈ D thì –x ∈ D và f(–x) = –f(x).

Comments

comments