![[Giải Toán 10] Chương 1: Mệnh đề – Tập hợp/ Bài 2: Tập hợp [Giải Toán 10] Chương 1: Mệnh đề – Tập hợp/ Bài 2: Tập hợp](https://lop12.edu.vn/wp-content/uploads/2019/10/t2.png)
Trả lời câu hỏi Toán 10 Đại số Bài 2 trang 10: Nêu ví dụ về tập hợp.
Dùng kí hiệu ∈ và ∉ để viết các mệnh đề sau.
a)3 là một số nguyên;
b)√2 không phải là số hữu tỉ
Lời giải
Ví dụ về tập hợp: Toàn bộ học sinh lớp 10A
a) 3 ∈ Z
b) √2 ∉ Q
Trả lời câu hỏi Toán 10 Đại số Bài 2 trang 10: Liệt kê các phần tử của tập hợp các ước nguyên dương của 30
Lời giải
A = {1; 2; 3; 5; 6; 10; 15; 30}
Trả lời câu hỏi Toán 10 Đại số Bài 2 trang 11: Tập hợp B các nghiệm của phương trình 2x2 – 5x + 3 = 0 được viết là B = { x ∈ R | 2x2 – 5x + 3 = 0}
Hãy liệt kê các phần tử của tập hợp B.
Lời giải
B = {3/2;1}
Trả lời câu hỏi Toán 10 Đại số Bài 2 trang 11: Hãy liệt kê các phần tử của tập hợp: A = { x ∈ R | x2 + x + 1 = 0}
Lời giải
Do phương trình x2 + x + 1 = 0 vô nghiệm nên tập hợp A không có phần tử nào
Trả lời câu hỏi Toán 10 Đại số Bài 2 trang 11: Biểu đồ minh họa trong hình nói gì về quan hệ giữa tập hợp các số nguyên Z và tập hợp các số hữu tỉ Q ? Có thể nói mỗi số nguyên là một số hữu tỉ hay không ?
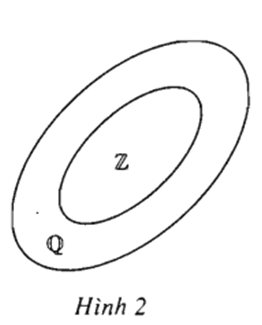
Lời giải
Tập hợp các số nguyên Z nằm trong tập hợp các số hữu tỉ Q
Có thể nói mỗi số nguyên là một số hữu tỉ
Trả lời câu hỏi Toán 10 Đại số Bài 2 trang 12: Xét hai trường hợp
A = { n ∈ N | n là bội của 4 và 6}
B = { n ∈ N | n là bội của 12}
Kiểm tra các kết luận sau
a)A ⊂ B b)B ⊂ A
Lời giải
Kết luận A đúng
Kết luận B đúng
Bài 1 (trang 13 SGK Đại số 10): a) Cho A = {x ϵ N | x < 20 và x chia hết cho 3}.
Hãy liệt kê các phần tử của A.
b) Cho B = {2, 6, 12, 20, 30}.
Hãy xách định B bằng cách chỉ ra một tính chất đặc trưng cho các phần tử của nó.
c) Hãy liệt kê các phần tử của tập hợp các học sinh lớp em cao trên 1m60.
Lời giải:
a) Tập hợp A là tập các số tự nhiên chia hết cho 3 và nhỏ hơn 20.
Vậy A = {0, 3, 6, 9, 12, 15, 18}
b) Nhận thấy: 2 = 1.2 ; 6 = 2.3 ; 12 = 3.4 ; 20 = 4.5 ; 30 = 5.6
Vậy B = {x = n(n + 1) | n ∈ N* và n ≤ 5}
c) Ví dụ: C = {Nam, Hoa, Anh, Linh}.
Kiến thức áp dụng
Có hai cách xác định tập hợp:
+ Liệt kê các phần tử của tập hợp.
+ Chỉ ra tính chất đặc trưng của chúng.
Bài 2 (trang 13 SGK Đại số 10): Trong hai tập hợp A, B dưới đây, tập hợp nào là tập hợp con của tập còn lại? Hai tập hợp A và B có bằng nhau không?
a) A là tập hợp các hình vuông;
B là tập hợp các hình thoi.
b) A = {n ∈ N | n là một ước chung của 24 và 30}.
B = { n ∈ N | n là một ước của 6}.
Lời giải:
a) Vì mỗi hình vuông đều là một hình thoi nên A ⊂ B.
Có những hình thoi không phải là hình vuông nên B ⊄ A.
Vậy A ≠ B.
b) A = {n ∈ N | n là một ước chung của 24 và 30} = {1; 2; 3; 6}.
B = {n ∈ N | n là một ước của 6} = {1; 2; 3; 6}.
Ta thấy A ⊂ B và B ⊂ A nên A = B.
Kiến thức áp dụng
+ Nếu mọi phần tử của A đều là phần tử của B thì ta nói A là tập con của B.
Kí hiệu A ⊂ B (một số tài liệu dùng kí hiệu A ⊆ B).
+ Nếu A ⊂ B và B ⊂ A thì A = B.
Bài 3 (trang 13 SGK Đại số 10): Tìm tất cả các tập con của tập hợp sau:
a) A = {a; b}
b) B = {0; 1; 2}
Lời giải:
a) A = {a; b} có các tập con: ∅; {a}; {b}; {a; b}
b) B = {0; 1; 2} có các tập con: ∅; {0}; {1} ; {2} ; {0, 1} ; {0, 2} ; {1, 2} ; {0; 1; 2}.
Kiến thức áp dụng
+ Tập rỗng là tập con của mọi tập hợp.
+ Mỗi tập hợp đều là tập con của chính nó.
+ Cách để kiểm tra xem viết đủ số lượng tập con chưa: Một tập hợp có n phần tử thì có 2n tập con.
Ví dụ tập A có 2 phần tử thì có 22 = 4 tập con.
tập B có 3 phần tử thì có 23 = 8 tập con.