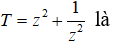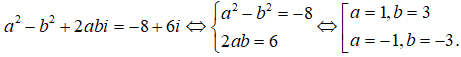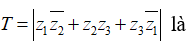
Câu 28: Môđun của số phức z = -1 + 7i là
A. 7 B. 6 C. √50 D. 8
Câu 29: Căn bậc hai của số phức z = -8 + 6i là
A. -1 – 3i và 1 + 3i B. -1 + 3i và 1 – 3i
C. 3 + i và -3 – i D. -3 + i và -3 – i.√2
Câu 30: Trên tập số phức, phương trình x2 + 2x + 3 = 0 có nghiệm là
A. 1 – √2i và 1 + √2i B. -1 – √2i và -1 + √2i
C. 1 + √2i và -1 + √2i D. 1 + √2i và -1 – √2i
Câu 31: Phương trình z2 + 4z + 7 có hai nghiệm z1, z2 . Giá trị của biểu thức T = |z1|2 + |z2|2 bằng
A. 7 B. 2√7 C. 14 D. 25
Câu 32: Cho các số phức z1 = -1 + i, z2 = 1 – 2i, z3 = 1 + 2i. Giá trị của biểu thức
![]()
A. 1 B. 3 C. 4 D. 5.
Câu 33: Tập hợp các điểm biểu diễn số phức z thỏa mãn z’ = (z + i)(z− + i) là một số thực và là đường thẳng có phương trình
A. x = 0 B. y = 0 C. x = y D. x = -y
Câu 34: Cho số phức z có môđun bằng 1. Giá trị nhỏ nhất của biểu thức
A. 2 B. 0 C. -2 D. -1
Hướng dẫn giải và Đáp án
| 28-C | 29-A | 30-B | 31-C | 32-D | 33-A | 34-C |
Câu 28:
![]()
Câu 29:
Ta có: z = -8 + 6i = 9i2 + 6i + 1 = (3i + 1)2
Do đó các căn bậc hai của z là ±(1 + 3i)
Chú ý: Có thể gọi căn bậc hai của z = -8 + 6i là w = a + bi (a, b ∈ R). Ta có:
w2 = a2 + 2abi + b2i2 = a2 – b2 + 2abi
Ta có:
Vậy các căn bậc hai của z = -8 + 6i là -1 – 3i và 1 + 3i
Câu 30:
Ta có: Δ’ = 12 – 3 = -2 = 2i2
Vậy phương trình có hai nghiệm là z1,2 = -1 ± √2i
Câu 31:
Ta có: Δ 4 – 7 = -3 = 3i2
Phương trình có hai nghiệm z1,2 = -2 ± i√3.
Vậy T = 2(√7)2 = 14
Câu 32:
Ta có: z1z2− + z2z3 + z3z1− + (1 – 2i)= (-1 + i)(1 + 2i) + (1 – 2i)(1 + 2i) + (1 + 2i)(-1 – i)
= (1 + 2i)( -1 + i -1 – i) + 1 – 4i2 = -2(1 + 2i) + 1 + 4 = 3 – 4i
![]()
Câu 33:
Đặt z = a + bi (a, b ∈ R). Ta có
z’ = [a + (b + 1)i][a – (b – 1)i] = a2 + (b – 1)2 + 2ai
Do đó z’ ∈ R <=> a = 0.
Vậy tập hợp các điểm M(a; b) biểu diễn số phức z là đường thẳng có phương trình z = 0
Câu 34:
Đặt z = a + bi (a, b ∈ R). Ta có |z| = 1 nên a2 + b2 = 1 và 1/z = z− = a – bi
Suy ra T = (a + bi)2 + (a – bi)2 = 2(a2 – b2) = 2(2a2 – 1) ≥ -2
Dấu “=” xảy ra khi a = 0. Vậy giá trị nhỏ nhất của T là -2