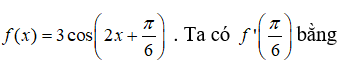
Câu 1: Đạo hàm của hàm số y = (x2 + 1)e3x là
A. 2x.e3x B. e3x(3x2 + 2x + 3) C. 3(x2 + 1)e3x D. 6xe3x
Câu 2: Cho hàm số
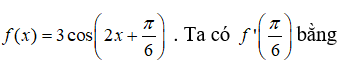
A. 0 B. –3 C. 6 D. -6
Câu 3: Cho hàm số y = x3 – 6x2 + 9x + 7. Hàm số đồng biến trên khoảng
A. (1; 3) B. (1; +∞) C. (-∞; 3) D. (-∞; 1) và (3; +∞)
Câu 4: Hàm số
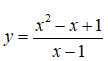
nghịch biến trên các khoảng
A. (0; 2) và (2; +∞) B. (-∞; 0) và (2; +∞)
C. [0; 1) và (1; 2] D. (0; 1) và (1; 2)
Câu 5: Hàm số nào trong các hàm số sau đây đồng biến trên R
A. y = x2 – 2x + 3 B. y = x3 + x
C. y = 1 + 1/(x2 + 1) D. y = ln(x2 + 1)
Câu 6: Hàm số y = x3 – 3x2 + mx + m đồng biến trên (-∞; +∞) khi và chỉ khi
A. m = 3 B. m ≥ 3 C. m ≤ 3 D. 0 ≤ m ≤ 3
Câu 7: Hàm số y = 2x3 – 9x2 + 12x – 4
A. Có cực đại mà không có cực tiểu B. Có cực tiểu mà không có cực đại
C. Không có cực đại và cực tiểu D. Có cả cực đại và cực tiểu.
Hướng dẫn giải và Đáp án
| 1-B | 2-D | 3-D | 4-C | 5-B | 6-B | 7-D |
Câu 1:
Ta có: y’ = (x2 + 1)’.33x + (x2 + 1)(e3x)’ = 2x.e3x + 3(x2 + 1)e3x = (3x2 + 2x + 3)e3x
Câu 2:
Ta có:
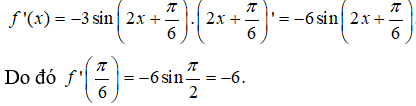
Câu 3:
Ta có: y’ = 3x2 – 12x + 9 = 3(x – 1)(x – 3), y’ > 0 <=> x ∈(-∞; 1) ∪ (3; +∞)
Vậy hàm số đồng biến trên các khoảng (-∞; 1) và (3; +∞) .
Câu 4:
Tập xác định: D = R\{1}. Ta có

y’ < 0 <=> x ∈ (0; 1) ∪ (1; 2)
Vậy hàm số nghịch biến trên các khoảng [0; 1 ) và (1; 2]
Câu 5:
Hàm số y = x2 – 2x + 3 có đồ thị là parabol nên không thể đồng biến trên R
Hàm số y = x3 + x xác định trên R và có đạo hàm y’ = 3x2 + 1 > 0, ∀x ∈ R nên đồng biến trên R .
Hàm số y = x2 + 1 đồng biến trên (0; +∞) nên hàm số
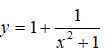
nghịch biến trên (0; +∞). Do đó hàm số
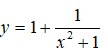
không thể đồng biến trên R .
Hàm số y = x2 + 1 nghịch biến trên (-∞; 0) nên hàm số y = ln(x2 + 1) nghịch biến trên khoảng (-∞; 0) . Do đó hàm số y = ln(x2 + 1) không thể đồng biến trên R .
Câu 6:
Ta có: y’ = 3x2 – 6x + m. Hàm số y = x3 – 3x2 + mx + m đồng biến trên (-∞; +∞) khi và chỉ khi y’ ≥ 0, ∀x ∈ (-∞; +∞) <=> m ≥ 3
Câu 7:
Ta có: y’ = 6x2 – 18x + 12 = 6(x – 1)(x – 2). Lập bảng biến thiên ta suy ra hàm số có cả cực đại và cực tiểu.