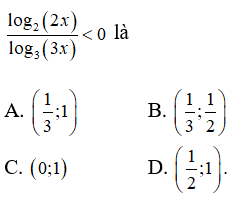
Câu 21: Tập hợp nghiệm của bất phương trình 3x + 4x > 5x là
A. (-∞; 2) B. (0; 2) C. (2; +∞) D. (0; 2]
Câu 22: Tập hợp nghiệm của bất phương trình
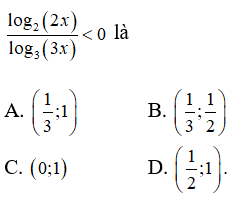
Câu 23: Tập hợp nghiệm của bất phương trình
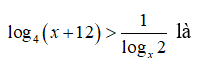
A. (-3; 4) B. (-3; 1) ∪ (1; 4) C. (0; 4) D. (0; 1) ∪ (1; 4)
Câu 24: Họ nguyên hàm của hàm số y = (2x + 1)5 là
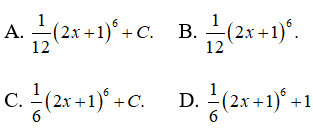
Câu 25: Diện tích của hình phẳng giới hạn bởi đường thẳng y = x và đường cong y = x2 bằng
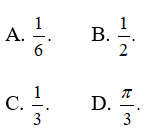
Câu 26: Thể tích của vật thể tròn xoay sinh ra bởi phép quay quanh trục Ox của hình phẳng giới hạn bởi các đường y = 4/x và y = -x + 5 là
A. 8π B. 9π C. 10π D. 12π
Câu 27: Số nào sau đây là số thuần ảo?
A. (2 + 3i)(2 – 3i) B. (2 + 3i) + (3 – 2i)
C. (2 + 3i) – 2(2 – 3i)
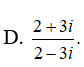
Hướng dẫn giải và Đáp án
| 21-B | 22-B | 23-D | 24-A | 25-A | 26-B | 27-C |
Câu 21:
Bất phương trình tương đương với
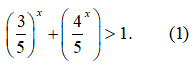
Do hàm số
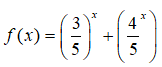
nghịch biến trên R và f(2) = 1 nên (1) tương đương với x < 2
Câu 22:
Điều kiện: x > 0, x ≠ 1/3. Khi đó ta có hai trường hợp:
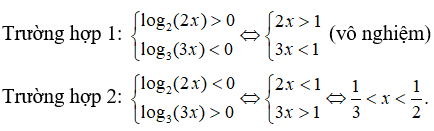
Vậy tập nghiệm của bất phương trình là (1/3; 1/2)
Câu 23:
Điều kiện: x > 0, x ≠ 1. Bất phương trình đã cho tương ứng với
(1/2)log2(x + 12) > log2x <=> x + 12 > x2 <=> 0 < x < 4
Kết hợp điều kiện ta có tập nghiệm của bất phương trình đã cho là (0; 1) ∪ (1; 4)
Câu 24:
Đặt t = 2x + 1. Ta có: dt = 2dx. Do đó:
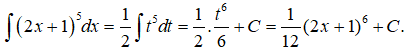
Câu 25:
Phương trình hoành độ giao điểm:
x = x2 <=> x = 0, x = 1
Diện tích cần tính là
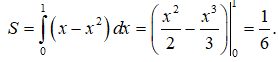
Câu 26:
Phương trình hoành độ giao điểm
4/x = -x + 5 <=> x2 – 5x + 4 = 0 <=> x = 1, x = 4
Thể tích cần tìm là
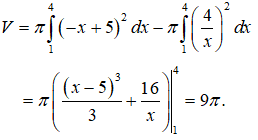
Câu 27:
Ta có:
(2 + 3i)(2 – 3i) = 4 – 9i2 = 13
(2 + 3i)+ (2 – 3i) = (2 + 2) + (3 – 3)i = 4
(2 + 3i) – (2 – 3i) = 2 – 2 + (3 + 3)i = 6i
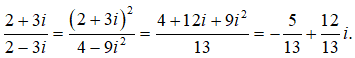
Vậy chỉ có (2 + 3i) – (2 – 3i) là số thuần ảo.