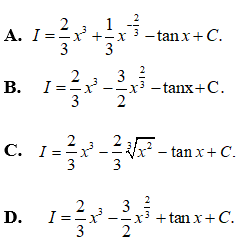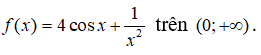
Câu 1: Trong các mệnh đề sau mệnh đề nào nhận giá trị đúng?

A. Hàm số y = 1/x có nguyên hàm trên (-∞; +∞).

B. 3x² là một số nguyên hàm của x³ trên (-∞; +∞).

C. Hàm số y = |x| có nguyên hàm trên (-∞;+∞).

D. 1/x + C là họ nguyên hàm của ln⁡x trên (0;+∞).

Câu 2: Hàm số nào dưới đây không phải là một nguyên hàm của f(x)=2x-sin⁡2x ?

x² + (1/2).cos⁡2x     B. x² + cos² x     C. x² – sin²x     D. x² + cos⁡2x .

Câu 3: Tìm nguyên hàm của

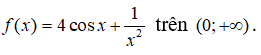
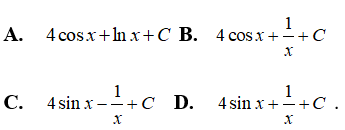
Câu 4:

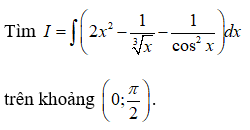
Hướng dẫn giải và Đáp án

Câu 1:

Dựa vào định lí: Mọi hàm số liên tục trên K đều có nguyên

hàm trên K. Vì y = |x| liên tục trên R nên có nguyên hàm trên R .

Phương án A sai vì y=1/x không xác định tại x=0 ∈ (-∞;+∞).

Phương án B sai vì 3x² là đạo hàm của x³.

Phương án D sai vì 1/x là đạo hàm của ln⁡x trên (0; +∞).

Vậy chọn đáp án C.

Câu 2:

Ta có

∫(2x-sin⁡2x)dx=2∫xdx-∫sin⁡2xdx

D không phải là nguyên hàm của f(x). Vậy chọn đáp án D.

Câu 3:

Với x ∈ (0; +∞) ta có

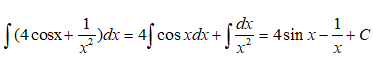
Vậy chọn đáp án C.

Câu 4:

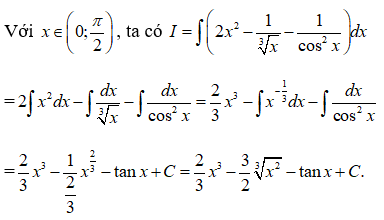
Vậy chọn đáp án B.

Ghi chú. Yêu cầu tìm nguyên hàm của một hàm số được hiểu là tìm nguyên hàm trên từng khoảng xác định của nó.

Comments

comments