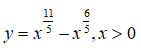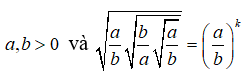
Câu 7: Giải bất phương trình log₃36 – log₃x > 1

A. 0 < x < 12    B. x < 12   C. x > 12    D. x < 1/12

Câu 8: Cho

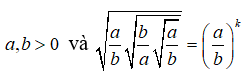
Tìm giá trị của k

Câu 9: Cho hàm số

Khẳng định nào sau đây là đúng?

A. Hàm số có hai điểm cực trị

B. Hàm số không có điểm cực trị nào

C. Hàm số có đúng một điểm cực trị và nó là điểm cực tiểu

D. Hàm số có đúng một điểm cực trị và nó là điểm cực đại

Câu 10: Tìm giá trị lớn nhất của hàm số y = ∛x(8 – x) trên đoạn [0; 8]

A. 4∛4   B. 5∛5    C. 6∛2    D. 10∛2

Câu 11: Nếu y = (log₂3)(log₃4)(log₄5)…(log₃₁32) thì

A. y = 5    B. 4 < y < 5    C. 5 < y < 6   D. y = 6

Câu 12: Đặt log80 = a, log45 = b . Hãy tính log36 theo a và b

A. a + b – 1   B. b – a + 1    C. a + b – 2   D. b – a + 2

Hướng dẫn giải và Đáp án

7-A

8-D

9-C

10-C

11-A

12-C

Câu 7:

log₃36 – log₃x > log₃36 – 1 > log₃x <=> log₃x < log₃36 – log₃3

<=> log₃x < log₃(36/3) <=> log₃x < log₃12 <=> 0 < x < 12

Câu 8:

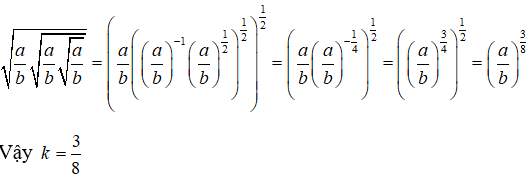
Câu 9:

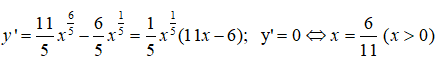
Ta thấy y’ đổi dấu từ âm sang dương khi đi qua x = 6/11 nên hàm số có đúng một điểm cực trị x = 6/11 và đó là điểm cực tiểu

Câu 10:

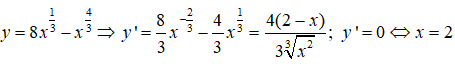
Ta có: y(0) = y(8) = 0, y(2) = 6∛2

Câu 11:

Sử dụng công thức log_ablog_bc = log_ca ta tính được

y = [(log₂3)(log₃4)](log₄5)…(log₃₁32) = [log₂4](log₄5)…(log₃₁32)

= [(log₂4)(log₄5)](log₅6)…(log₃₁32) = [log₂3](log₅6)…(log₃₁32)

= … = log₂32 = log₂2⁵ = 5

Cách khác:

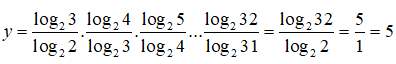
Câu 12:

Ta có: log36 = log(2².3²) = 2(log2 + log3)

log80 = a => 3log2 + 1 = a => log2 = (a-1)/3

log45 = b => b = log(3².5) = 2log3 + log5 = 2log3 + log(10/2) = 2log3 + 1 – log2

=> 2log3 = b – 1 + log2 = b – 1 + (a – 1)/3 = b + (a/3) – (4/3)

Từ đó:

Comments

comments