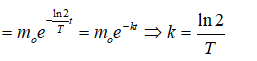Câu 15: Nếu a = log₈225 và b = log₂15 thì giữa a và b có hệ thức

Câu 16: Khối lượng m của một chất phóng xạ thay đổi theo thời gian t tuân theo công thức

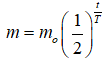
trong đó m₀ là khối lượng chất phóng xạ ban đầu, T là chu kì bán rã. Nếu viết phương trình này dưới dạng m = m₀e^-ktthì :

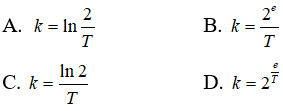
Câu 17: Đặt log₈3 = p và log_nx = 3log_mx . Hãy biểu thị log5 theo p và q

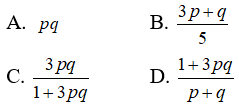
Câu 18: Cho m, n > 1 và log_nx = 3log_mx với mọi x > 0. Hãy biểu thị m theo n

A. m = n³    B. m = 1/n³   C. m = ∛n    D. m = 1/∛n

Câu 19: Biết rằng 4^a = 5, 5^b = 6, 6^c = 7, 7^d = 8. Tính abcd

A. 1/2    B. 3/2    C. 2   D. 2/3

Câu 20: Cho b > 1, sinx > 0, cosx > 0 và log_bsinx = a. Khi đó log_bcosx bằng

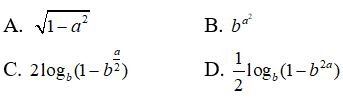
Hướng dẫn giải và Đáp án

Câu 15:

a = log₈225 = log_2³15² = (2/3)log₂15 = 2b/3

Câu 16:

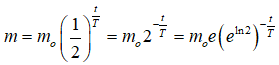
Câu 17:

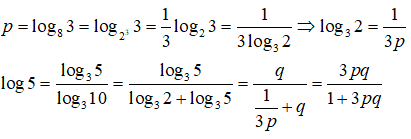
Câu 18:

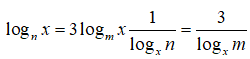
=> log_xm = 3log_xn = log_xn³ => m = n³

Câu 19:

Từ giả thiết ta có: a = log₄5, b = log₅6, c = log₆7, d = log₇8

=> abcd = log₄5.log₅6.log₆7.log₇8 = log₄6log₆7log₇8 = log₄7.log₇8 = log₄8 = log_2²2³ = (3/2)log₂2 = 3/2

Câu 20:

log_bsinx = a => sin x = b^a => sin²x = b^2a => cosx = (1 – b^2a)^1/2)

=> log_bcosx = (1/2)log_b(1 – b^2a)

Comments

comments