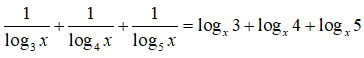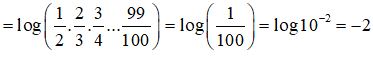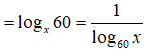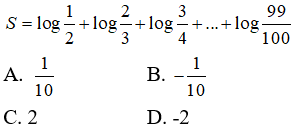
Câu 8: Biết rằng log₃y = (1/2)log₃u + log₃v + 1. Hãy biểu thị y theo u và v

A. y = 3√uv    B. y = 3u²v    C. y = 3 + √u + v    D. y = (√uv)³

Câu 9: Tìm số k sao cho 2^x = e^kx với mọi số thực x

A. k = √2    B. k = 2^x   C. k = log₂e    D. k = ln2

Câu 10: Độ pH của một chất được xác định bởi công thức pH = -log[H⁺] trong đó H⁺ là nồng độ ion hyđrô trong chất đó tính theo mol/lít (mol/L). Xác định nồng độ ion H⁺ của một chất biết rằng độ pH của nó là 8,06

A. 8,7.10^-9 mol/L    B. 2,44.10^-7 mol/L

C. 2,74,4 mol/L    D. 3,6.10^-7 mol/L

Câu 11: log125 bằng

A. 5log3    B. 3 – 3log2    C. 100log1,25    D. (log25)(log5)

Câu 12: Cho a, b, c là các số dương. Tính giá trị của biểu thức log_ab².log_bc².log_ca²

A. 1/8    B. 1   C. 8   D. 6

Câu 13: Tính giá trị của biểu thức

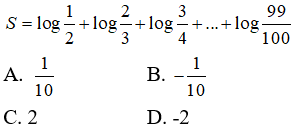
Câu 14: Với 0 < x ≠ 1 , biểu thức

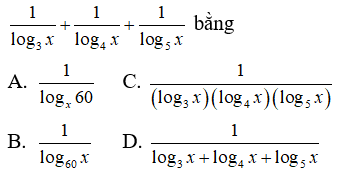
Hướng dẫn giải và Đáp án

Câu 8:

log₃y = (1/2)log₃u + log₃v + 1 <=> log₃y = log₃u^1/2 + log₃v + log₃3 = log₃(√u.v.3) => y = 3√u.v

Câu 9:

Ta có: 2^x = (e^ln2)x = e^xln2 = e^kx => k = ln2

Câu 10:

pH = -log[H⁺] => [H⁺] = 10^-pH = 10^-8,06 ≈ 8,76.10^-9(mol/L)

Câu 11:

log125 = log(1000/8) = log1000 – log8 = log10³ – log2³ = 3 – 3log2

Câu 12:

log_ab².log_bc².log_ca² = (2log_ab)(2log_bc)(2log_ca) = 8log_ab.log_bc.log_ca = 8log_ac.log_ca = 8

Câu 13:

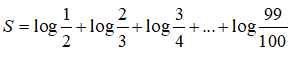
Câu 14:

Comments

comments