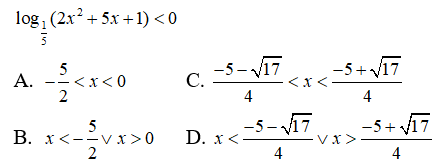
Câu 8: Giải bất phương trình log5(2x – 4) < log5(x + 3)
A. 2 < x < 7 B. -3 < x < 7 C. -3 < x < 2 D. x < 7
Câu 9: Giải bất phương trình ln(xx – 2x – 2) < 0
A. -1 ≥ x ≥ 3 C. x ∞[-1; 1 – √3) ∪ (1 + √3)
B. -1 – √3 < x < 1 + √3 D. x ∞ (1 + √3), 3]
Câu 10: Giải bất phương trình
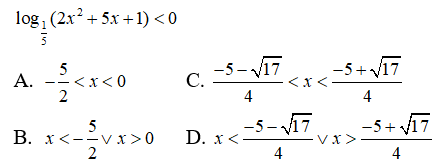
Câu 11: Giải bất phương trình logx + log(x + 9) > 11
A. 0 < x < 3 C. x < 1 hoặc x > 2
B. x < 0 hoặc x > 3 D. 0 < x < 1 hoặc 2 < x < 3
Câu 12: Giải bất phương trình 3log2(x2 – 3x + 2) > 3
A. 0 < x < 3 C. x < 1 hoặc x > 2
B. x < 0 hoặc x > 3 D. 0 < x < 1 hoặc 2 < x < 3
Câu 13: Tìm miền xác định của hàm số y = ln(lnx)
A. D = (e; +∞) B. D = [e; ∞) C. D = (0; +∞) D. D = (1; +∞)
Câu 14: Tìm khoảng đồng biến của hàm số y = xlnx
A. (0; 1/e) B. (0; e) C. (1/e; +∞) D. (e; +∞)
Hướng dẫn giải và Đáp án
| 8-A | 9-D | 10-B | 11-A | 12-B | 13-D | 14-C |
Câu 8:
log5(2x – 4) < log5(x + 3)
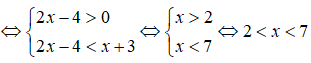
Câu 9:
Điều kiện
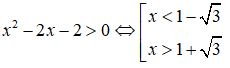
Khi đó BPT <=> x2 – 2x – 2 ≤ e0 = 1 <=> x2 – 2x – 3 ≤ 0 <=> -1 ≤ x ≤ 3
Kết hợp được tập nghiệm: (1 + √3; 3)
Câu 10:
log1/5(2x2 + 5x + 1) < 0 <=> 2x2 + 5x + 1 > 1 (do 0 < 1/5 < 1)
<=> 2x2 + 5x > 0 <=> x < -2/5 hoặc x > 0
Câu 11:
Điều kiện x > 0. Khi đó bất phương trình đã cho tương đương với
log[x(x + 9)] > 1 <=> x(x + 9) > 10 <=> x2 + 9x – 10 > 0
<=> x < -10 hoặc x > 1 <=> x > 1 (do x > 0)
Câu 12:
3log2(x2 – 3x + 2) > 3 7lt;=> log2(x2 – 3x + 2) > 1 <=> x2 – 3 + 2 > 2
<=> x2 – 3x > 0 <=> x < 0 hoặc x> 3
Câu 13:
Điều kiện ln > 0 <=> x > e0 = 1
Câu 14:
Tập xác định: (0; +∞). y’ = lnx + 1 > 0 <=> lnx > -1 <=> x > 1/e