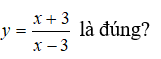
Câu 1: Kết luận nào sau đây về tính đơn điệu của hàm số
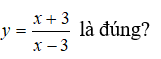
A. Hàm số đồng biến trên các khoảng (-∞; 3) và (3; +∞) .
B. Hàm số luôn đồng biến trên R\{3}
C. Hàm số nghịch biến trên các khoảng (-∞; 3) và (3; +∞)
D. Hàm số luôn nghịch biến trên R\{3}
Câu 2: Tìm khoảng nghịch biến của hàm số sau: y = -x4 – 2x3 + 3
A. (-∞; 0) B. (0; +∞) C. R D. (1; +∞)
Câu 3: Tìm m để hàm số
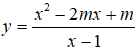
tăng trên từng khoảng xác định của
A. m ≥ 1 B. m ≠ 1 C. m > 1 D. m ≤ 1
Câu 4: Tìm giá trị lớn nhất của m để hàm số y = x3 + 3x2 – mx – 4 đồng biến trên khoảng (-∞; 0)
A. m = -3 B. m < -3 C. m ≤ -3 D. m ≥ -3
Câu 5: Hàm số
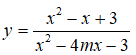
có tất cả bao nhiêu đường tiệm cận?
A. 1 B. 2 C. 3 D. 4
Câu 6: Cho hàm số y = x3 – 3x2 + 1. Tích của giá trị cực đại và cực tiểu của hàm số bằng bao nhiêu?
A. -6 B. -3 C. 3 D. 4
Hướng dẫn giải và Đáp án
| 1-C | 2-B | 3-A | 4-A | 5-C | 6-B |