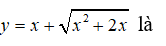
Câu 7: Đường tiệm cận ngang của đồ thị hàm số
![]()
A.y = 1 B. y = 0 C. y = -1 D. Không tồn tại
Câu 8: Đường tiệm cận đứng của đồ thị hàm số
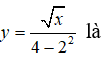
A. x = 0 B. x = 2, x = -2 C. x – 2 = 0 D. x + 2 = 0
Câu 9: Cho hàm số
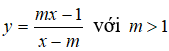
Hỏi giao điểm của hai đường tiệm cận của đồ thị hàm số trên luôn nằm trên một đường cố định có phương trình nào trong các phương trình sau?
A. y = x B. x2 + y2 = 1 C. y = x2 D. y = x3
Câu 10: Đồ thị hàm số y = x3 – mx2 + 2 có tất cả bao nhiêu đường tiệm cận?
A. 1 B. 2 C. 0 D. 3
Câu 11: Đồ thị hàm số
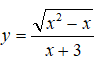
có tất cả bao nhiêu đường tiệm cận?
A. 1 B. 2 C. 3 D. 4
Câu 12: Đồ thị hàm số
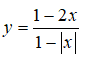
có tất cả bao nhiêu đường tiệm cận?
A. 1 B. 2 C. 3 D. 4
Câu 13: Tìm m để đồ thị hàm số
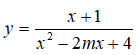
có ba đường tiệm cận
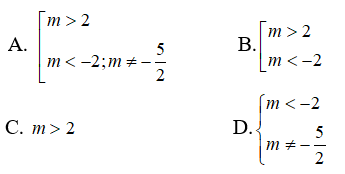
Hướng dẫn giải và Đáp án
| 7-C | 8-C | 9-A | 10-C | 11-D | 12-A |
Câu 7:
Ta có
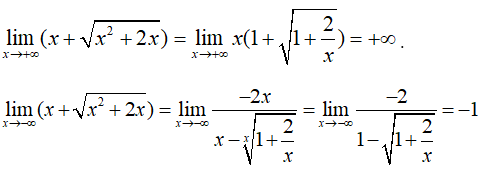
=> y= -1 là tiệm cận ngang của đồ thị hàm số .
Câu 8:
Ta có
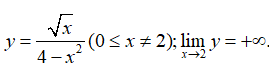
Do đó x – 2 = 0 là tiệm cận đứng của đồ thị hàm số.
Câu 9:
y = m là tiệm cận ngang, x = m là tiệm cận đứng của đồ thị hàm số. Vậy giao điểm hai tiệm cận là I(m;m). Dễ dàng nhận thấy I thuộc đường thẳng có phương trình y=x.
Câu 11:
x= -3; y=1; y= -1 là ba đường tiệm cận của đồ thị hàm số.
Câu 13:
Đồ thị hàm số có ba đường tiệm cận chỉ khi phương trình x2 -2mx + 4 = 0 có hai nghiệm phân biệt khác -1.