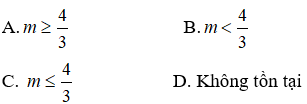
Câu 7: Với giá trị nào của m, hàm số y = x3 – 2x2 + mx – 1 không có cực trị?
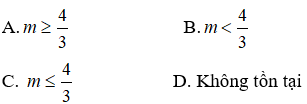
Câu 8: Với giá trị nào của m, hàm số y = -mx4 + 2(m – 1)x2 + 1 – 2m có một cực trị
A.0 ≤ m ≤ 1 B. m > 1 hoặc m < 0 C. 0 < m < 1 D. 0 < m ≤ 1
Câu 9: Giá trị của m để hàm số y = x3 – 3mx2 + (m2 – 1)x + 2 đạt cực đại tại x = 2 là:
A. m = 1 B. m = 11 C. m = -1 D. Không tồn tại
Câu 10: Với giá trị nào của m, hàm số y = (x – m)3 – 3x đạt cực tiểu tại điểm có hoành độ x = 0?
A. m = 1 B. m = -1 C. m = 0 D. Không tồn tại
Câu 11: Với giá trị nào của m, hàm số y = x3 + 2(m – 1)x2 + (m2 – 4m + 1)x + 2(m2 + 1) có hai điểm cực trị x1,x2 thỏa mãn
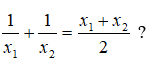
A. m = 1/2 B. m = 2 C. m = 1/2 hoặc m = 2 D. Không tồn tại
Câu 12: Với giá trị nào của m, đồ thị hàm số y = x3 – mx2 + 3(m2 – 1)x – m 3 + m có điểm cực đại B, điểm cực tiểu C thỏa mãn OC = 3OB, với O là gốc tọa độ?
Hướng dẫn giải và Đáp án
| 7-A | 8-A | 9-B | 10-B | 11-C | 12-C |
Câu 7:
y’ = 3x2 – 4x + m. Hàm số không có cực trị <=> y’=0 vô nghiệm hoặc có nghiệm kép <=> Δ’ ≤ 0 <=> 22 – 3m ≤ 0 <=> m ≥ 4/3
Do đó hàm số không có cực trị khi m ≥ 4/3
Câu 8:
Xét hàm số y = -mx4 +2(m – 1)x2 + 1 – 2m(1)
TH1: m = 0 (1) trở thành y = -2x2 + 1
Vậy với m = 0 hàm số luôn có một cực trị.
TH2: m ≠ 0. y’ = -4mx3 + 4(m – 1)x
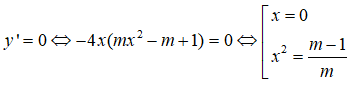
Để hàm số (1) có một cực trị thì
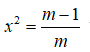
vô nghiệm hoặc có nghiệm kép bằng 0
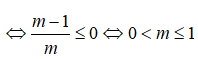
Kết hợp cả hai trường hợp ta có 0 ≤ m ≤ 1
Câu 9:
y’ = 3x2 – 6mx + m2 – 1; y” = 6x – 6m
Hàm số đạt cực đại tại x = 2 khi
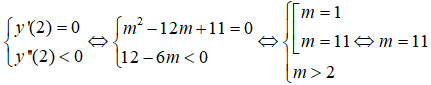
Câu 10:
Xét y = x3 – 3mx2 + (3m2 – 3)x – m2
Ta có: y’ = 32 – 6mx + 3m2 – 3, y” = 6x – 6m
Hàm số đạt cực tiểu tại điểm có hoành độ x = 0 khi
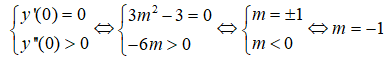
Câu 11:
Ta có y’ = 3x2 + 4(m – 1)x + m2 – 4m + 1. Hàm số có hai cực trị
=> y’ = 0 có hai nghiệm phân biệt <=> Δ’ > 0 <=> 4(m – 1)2 – 3(m2 – 4m + 1) > 0
<=> m2 + 4m + 1 > 0
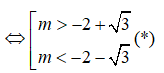
Áp dụng Vi-ét cho phương trình y’ = 0 có hai nghiệm phân biệt x1, x2 ta có :
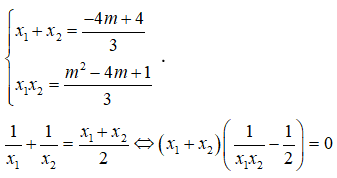
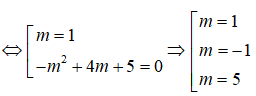
Đối chiếu điều kiện (*) có m = 5 hoặc m = 1
Câu 12:
Ta có y’ = 3x2 – 6mx + 3(m2 – 1).
Hàm số có hai cực trị => y’ = 0 có hai nghiệm phân biệt <=> Δ’ > 0 <=> (3m)2 – 3.3(m2 – 1) > 0 <=> 9 > 0 đúng với mọi m. Ta có điểm cực đại là B(m – 1; -2m + 2) và cực tiểu là C(m + 1; -2m – 2)
![]()
<=> 40m2 – 100m + 40 = 0
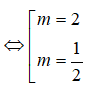
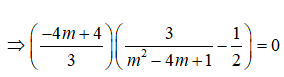
1families
gay universe chat https://bjsgaychatroom.info/
gay dating advice – dating a much younger man or 18 yr old in high school https://gaypridee.com/
kik chat gay penis https://gaytgpost.com/
random gay cam chat https://gay-buddies.com/
about dating gay spanish men https://speedgaydate.com/
las vegas slots https://freeonlneslotmachine.com/
huge casino slots https://candylandslotmachine.com/
slots era https://pennyslotmachines.org/
hollywood slots in bangor https://slotmachinesworld.com/
caesars slots free https://beat-slot-machines.com/
triple seven slots free https://download-slot-machines.com/
slots online https://www-slotmachines.com/
free adult slots online https://slotmachinegameinfo.com/
dissertation proposal defense powerpoint https://buydissertationhelp.com/
professional dissertation writers https://dissertationwriting-service.com/
dissertation proposal help https://help-with-dissertations.com/
liberty university dissertation template https://mydissertationwritinghelp.com/
writing dissertation books https://helpon-doctoral-dissertations.net/
Comments are closed.