
Khi nhận đề thi Toán, thí sinh đọc câu hỏi và xác định được từ khóa quan trọng để liên hệ với các công thức, tìm được hướng giải.
Học sinh thi tốt nghiệp THPT môn Toán chiều 9/8. Cấu trúc đề năm nay không khác nhiều so với kỳ thi THPT quốc gia năm trước nhưng mức độ câu hỏi sẽ dễ hơn. Trong đó, khoảng 10 câu yêu cầu vận dụng cao để phân loại thí sinh.
Thầy Lâm Vũ Công Chính (giáo viên Toán trường THPT Nguyễn Du) lưu ý thí sinh một số vấn đề có thể làm tốt bài thi.
Thứ nhất, trong đề thi, các câu hỏi được sắp xếp theo mức độ từ dễ tới khó nên đừng vội làm những câu khó đầu tiên. Một khởi đầu tốt sẽ mang lại nhiều năng lượng trong suốt quá trình thi. Sẽ đủ thời gian để giải quyết những câu cơ bản và thời gian còn lại để các em làm các câu hỏi vận dụng cao.
Do vậy, thí sinh cần làm bài thật cẩn thận, chính xác. Một sai sót nhỏ có thể khiến kết quả thi không được như ý muốn.
Thứ hai, khi đọc câu hỏi cần xác định được từ khóa quan trọng, để liên hệ được các công thức liên quan và tìm được hướng giải. Đó cũng là cách hệ thống kiến thức khi ôn tập.
Những bài toán liên quan đến cực trị của hàm số, cần chú ý đến thuật ngữ cực đại của hàm số và điểm cực đại của hàm số. Hoặc liên quan đến đường tiệm cận của đồ thị hàm số, thí sinh cần phân biệt được tiệm cận đứng và tiệm cận ngang, điều kiện để đường thẳng là tiệm cận của đồ thị hàm số.
Ví dụ:

Ở đây học sinh có thể chọn đáp án là 2 vì đường tiệm cận đứng là x = 1 và x = – 1.
Tuy nhiên do tập xác định của hàm số không chứa x = -1 nên chỉ có một đường tiệm cận đứng là x = 1. Cũng như có học sinh sẽ chọn cả tiệm cận ngang vào đáp án.
Thí sinh cần đọc kỹ câu hỏi, ví dụ Tìm số phức liên hợp của số phức z thỏa mãn điều kiện… thì sau khi tìm được số phức z phải tìm ra số phức liên hợp của z theo yêu cầu của đề bài.
Ngoài ra các em cần lưu ý một số tính chất đặc trưng, từ đó có những công thức tính nhanh. Ví dụ, dựa vào dấu của hệ số a và b của hàm trùng phương có thể kết luận được số cực trị của hàm số, hoặc công thức tính nhanh độ dài cạnh, tính diện tích của các tam giác đặc biệt…
Thứ ba, thí sinh có thể sử dụng các phương pháp loại suy, thử sai, kiểm chứng đáp án để làm bài trắc nghiệm cũng như sử dụng các tính năng của máy tính cầm tay để giải quyết bài toán. Tuy nhiên hạn chế của máy tính cầm tay là bộ nhớ có giới hạn, tính năng bảng (TABLE) chỉ quét được các giá trị theo bước nhảy (STEP) có thể bỏ sót những giá trị quan trọng của bài toán.
Ví dụ:
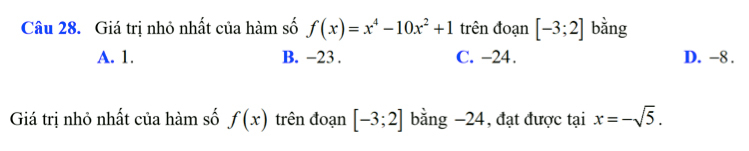
Nhưng nếu học sinh sử dụng tính năng bảng (TABLE) có thể sẽ dẫn đến kết quả sai là -23.
Thứ tư, số câu hỏi liên quan đến kiến thức lớp 10 và 11 tuy không nhiều, nhưng cần ôn tập nghiêm túc vì các câu hỏi này không quá khó – tập trung vào phần dãy số, cấp số cộng, cấp số nhân, đại số tổ hợp, xác suất, nhị thức Newton…
Các câu hỏi vận dụng cao ở cuối đề thi không nhất thiết xếp theo độ khó tăng dần, có khi “khó người, dễ ta” nếu thí sinh từng tham khảo qua lời giải của những bài toán tương tự. Đây cũng là yếu tố phân định khả năng lọt qua “cửa hẹp” để bước vào cánh cửa đại học.
Cuối cùng ‘gần ngày thi nên làm gì?’ là câu hỏi đặt ra cho nhiều sĩ tử. Các em chẳng cần phải thắp nến ôn thi ngày đêm, thở bình oxy trong phòng đóng kín như áp lực của Gaokao – kỳ thi đại học ở Trung Quốc. Bởi làm gì cũng cần một quá trình. Thế nên các em chỉ cần duy trì những gì đang có, ôn tập đều đặn và đầy đủ các kiến thức cơ bản. Con đường dẫn đến thành công phải đi trên đôi chân kiên trì, nhẫn nại.
Theo VNE