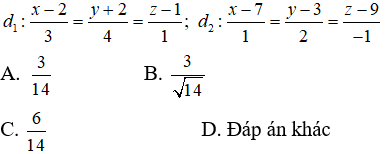
Câu 33: Tính khoảng cách giữa hai đường thẳng chéo nhau sau đây
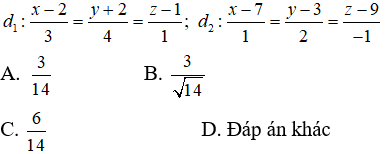
Câu 34: Trong không gian Oxyz, cho đường thẳng
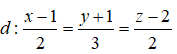
và mặt phẳng 2x – 2y + z + 3 = 0. Tính khoảng cách giữa d và (P)
A. 0 B. 3 C. 1 D. 9
Câu 35: Trong không gian Oxyz, lập phương trình chính tắc của mặt cầu (S) có tâm là I(1;0;-1) và tiếp xúc với đường thẳng
![]()
A. (x – 1)2 + y2 + (z + 1)2 = 81 C. (x + 1)2 + y2 + (z – 1)2 = 81
B. (x – 1)2 + y2 + (z + 1)2 = 9 D. (x – 1)2 + y2 + (z + 1)2 = 3
Câu 36: Trong không gian Oxyz, lập phương trình chính tắc của mặt cầu (S) có tâm là I(1;0;-1) và cắt đường thẳng
![]()
theo một dây cung AB có độ dài bằng 8
A. (x – 1)2 + y2 + (z + 1)2 = 16 C. (x – 1)2 + y2 + (z + 1)2 = 25
B. (x – 1)2 + y2 + (z + 1)2 = 5 D. (x + 1)2 + y2 + (z – 1)2 = 25
Câu 37: Trong không gian Oxyz, cho hai điểm A(-2; -2; -4), M(1; 0; 0) . Lập phương trình đường thẳng d đi qua điểm M, nằm trong mặt phẳng (P): x + y + z – 1 = 0 sao cho khoảng cách từ A đến đường thẳng d đạt giá trị lớn nhất
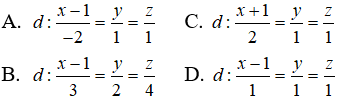
Câu 38: Trong không gian Oxyz, cho hai điểm A(2; 0; 1), B(8; 4; -5) và mặt phẳng 2x + 2y – z + 1 = 0 . Tìm tọa độ của điểm M thuộc mặt phẳng (P) sao cho AM2 + BM2 đạt giá trị nhỏ nhất
A. M(1; -2; -1) B. M(9; 6; -5) C. M(1; -2; -5) D. Đáp án khác
Câu 39: Trong không gian Oxyz, cho mặt cầu (S) có phương trình là: (x + 1)2 + (y – 4)2 + (z + 3)2 = 36 . Số mặt phẳng (P) chứa trục Ox và tiếp xúc với mặt cầu (S) là:
A. 0 B. 1 C. 2 D. Vô số
Câu 40: Trong không gian Oxyz, cho ba điểm A(0; 0; 0), B(1; 2; 3), C(2; 3; 1). Gọi D là chân đường phân giác trong xuất phát từ đỉnh A của tam giác ABC. Trong các khẳng định dưới đây, khẳng định nào sai?
A. AD ⊥ BC
B. Một vectơ chỉ phương của đường thẳng AD là: AB→ + AC→
C. Một vectơ chỉ phương của đường thẳng AD là:
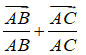
D. Một vectơ chỉ phương của đường thẳng AD là: uAD→ = (1; 1; -2)
Hướng dẫn giải và Đáp án
| 33-B | 34-B | 35-B | 36-C | 37-A | 38-A | 39-A | 40-D |
Câu 35:
Đường thẳng d đi qua điểm M(6 ;1 ;0) và có vectơ chỉ phương là ud→ = (4; -1; -1). Ta có :
![]()
Do đường thẳng d tiếp xúc với mặt cầu (S) nên (S) có bán kính là :
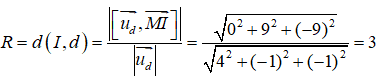
Vậy phương trình của mặt cầu (S) là : (x – 1)2 + y2 + (z + 1)2 = 9
Câu 36:
Đường thẳng d đi qua điểm M(-2 ;3 ;2) và có vectơ chỉ phương là ud→ = (-4; 1; 1) Ta có :
![]()
Khoảng cách từ I đến đường thẳng d là :
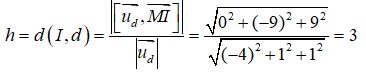
Do d cắt (S) theo dây cung AB có độ dài bằng 8 nên ta có:
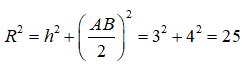
Vậy phương trình của mặt cầu (S) là: (x – 1)2 + y2 + (z + 1)2 = 25
Câu 37:
Gọi H là hình chiếu vuông góc của A trên d. Ta có: d(A; d) = AH ≤ AM = √29
Dấu bằng xảy ra khi và chỉ khi H trùng M, nghĩa là d vuông góc với AM.
Từ đó ta được
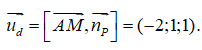
Vậy d có phương trình là:
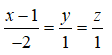
Câu 39:
Mặt cầu (S) có tâm I(-1;4;-3) và có bán kính R = 6. Gọi H là hình chiếu vuông góc của I trên trục Ox. Ta có H(-1;0;0) và IH=5.
Gọi K là hình chiếu vuông góc của I trên mặt phẳng (P). Ta có
d(I; (P)) = IK ≤ IH = 5 < R = 6
Do đó mặt phẳng (P) luôn cắt mặt cầu (S) theo một đường tròn. Vậy không tồn tại mặt phẳng (P) chứa Ox và tiếp xúc với (S)
Câu 40:
Ta thấy tam giác ABC cân tại đỉnh A, do đó các khẳng định A, B và C đều đúng. Vậy khẳng định D sai.