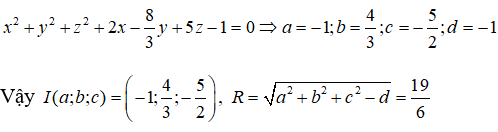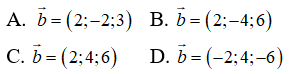
Câu 31: Trong không gian Oxyz, cho vectơ a→ = (-1; -2; 3) . Tìm tọa độ của vectơ b→ = (2; y; z) biết rằng vectơ b→ cùng phương với vectơ a→
Câu 32: Trong không gian Oxyz, cho vectơ a→ = (m; m + 3; 3 – 2m). Với giá trị nào của m thì vectơ a→ có độ dài nhỏ nhất
A. m = 1/2 B. m = 0 C. m = 1 D. m = -3
Câu 33: Trong không gian Oxyz, cho hai vectơ u→ = (3; 4; 0), v→ = (2; -1; 2) . Tích vô hướng của hai vectơ u→ và v→ là:
A. 15 B. 2 C. 3 D. 0
Câu 34: Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
(x – 1)2 + (y + 2)2 + (z + 3)2 = 25
Tìm tọa độ tâm I và bán kính R của mặt cầu (S)
A. I(1; -2; -3); R = 25 C. I(-1; 2; 3); R = 25
B. I(-1; 2; 3); R = 5 D. I(1; -2; -3); R = 5
Câu 35: Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
x2 + y2 + z2 – 2x + 4y + 4z + 5 = 0
Tìm tọa độ tâm I và bán kính R của mặt cầu (S)
A. I(1; -2; -2); R = 2 C. I(-1; 2; 2); R = 2
B. I(1; -2; -2); R = 4 D. I(-2; 4; 4); R = 4
Câu 36: Phương trình nào dưới đây là phương trình của một mặt cầu?
A. x2 + y2 + z2 – 2x + 4y – 8z – 25 = 0
B. x2 + y2 + z2 – 2x – 4y – 6z + 15 = 0
C. 3x2 + 3y2 + 3z2 – 6x – 7y – 8z + 1 = 0
D. (x – 1)2 + (y + 2)2 + (z + 3)2 + 10 = 0
Câu 37: Trong không gian Oxyz, cho mặt cầu (S) có phương trình là:
3x2 + 3y2 + 3z2 + 6x – 8y + 15z – 3 = 0
Tìm tọa độ tâm I và bán kính R của mặt cầu (S).
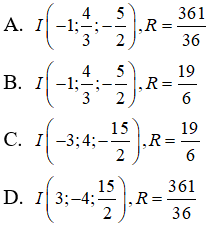
Hướng dẫn giải và Đáp án
| 31-D | 32-A | 33-B | 34-D | 35-A | 36-C | 37-B |
Câu 31:
Vectơ b→ cùng phương với vectơ a→ khi và chỉ khi tồn tại một số thực k thỏa mãn:
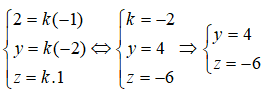
Câu 36:
Sử dụng phương trình x2 + y2 + z2 – 2ax – 2by – 2cz + d = 0 là phương trình của một mặt cầu khi và chỉ khi: a2 + b2 + c2 – d > 0
Câu 37:
Phương trình (S) được viết lại dưới dạng: