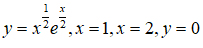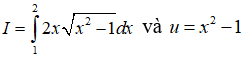
Câu 34: Cho
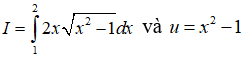
Khẳng định nào sai?

Câu 35: Biến đổi
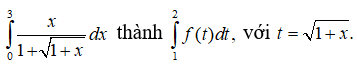
Khi đó, f(t) là hàm nào trong các hàm số sau?
A. f(t) = 2t2 – 2t B. f(t) = t2 + t C. f(t) = t2 – t D. f(t) = 2t2 + 2t
Câu 36: Diện tích hình giới hạn bởi đường cong y = x2 + 1 tiếp tuyến với đường cong này tại M(2; 5) và trục là:
A. 0 B. -8/3 C. 8/3 D. Kết quả khác.
Câu 37: Thể tích vật tròn xoay khi quay hình phẳng giới hạn bởi các đường y = 4/x, y = 0, x = 1, x = 4 quanh trục Ox là:
A. 6π B. 4π C. 12π D. 8π
Câu 38: Thể tích vật tròn xoay khi quay hình phẳng giới hạn bởi các đường
quanh trục Ox là:
A. π(e2 + e) B. π(e2 – e) C. πe2 D. πe
Câu 39: Phần thực và phần ảo của số phức z thỏa mãn z− = (1 + 2i)2 + (1 – 2i)3 là
A. 14 và 6i B. –14 và 6 C. 14 và – 6 D. –14 và –6.
Câu 40: Thực hiện phép tính T = 3i(5 + 2i) + (2 – 5i)(3 + 7i) ta có:
A. T = 35 + 14i B. T = 35 – 24i C. T = -35 + 14i D. T = -35 – 14i
Hướng dẫn giải và Đáp án
| 34-A | 35-A | 36-C | 37-C | 38-C | 39-D | 40-A |
Câu 34:
Dễ thấy B, C, D là các khẳng định đúng, còn khẳng định A sai vì đổi biến mà không đổi cận
Câu 35:
Ta có:
![]()
Câu 36:
Phương trình tiếp tuyến với y = x2 + 1 tại M(2 ;5) là :
y = y'(2)(x – 2) + 5 => y = 4(x – 2) + 5 = 4x – 3
Xét PT : x2 + 1 = 4x – 3 => x = 2 . Ta có
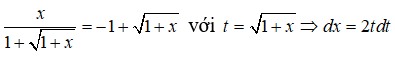
Câu 37:
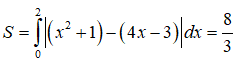
Câu 38:
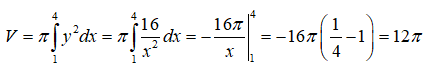
Câu 39:
Ta có: z− = (1 + 2i)2 + (1 – 2i)3 = 1 + 4i – 4 + 1 – 6i – 12 + 8i = -14 + 6i
Suy ra z = -14 – 6i. Vậy phần thực và phần ảo của z là: -14 và – 6
Câu 40:
Ta có: T = 15i + 6i2 + 6 + 14i – 15i – 35i2 = 15i – 6 + 6 + 14i – 15i + 35 = 35 + 14i