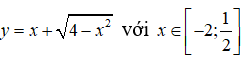
Câu 13: Hàm số

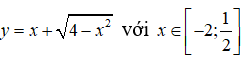
đạt giá trị lớn nhất tại x bằng

A. 1    B. 1/2    C. -2   D. -1.

Câu 14: Tìm m để đồ thị hàm số y = x⁴ – 2m²x² + 1 có ba cực trị tạo thành tam giác vuông.

A. m = ± 1   B. m = ± 2     C. m = 3    D. Đáp án khác.

Câu 15: Tính giá trị biểu thức log₃5.log₄9.log₅2

A. 1/2    B. 1   C. 2   D. 3

Câu 16: Tìm đạo hàm của hàm số y = (√3)^x2

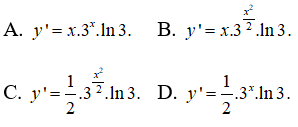
Câu 17: Nếu 4^x – 4^{x – 1} = 24 thì (2x)^x bằng

A. 5√5   B. 25   C. 25√5   D. 125.

Câu 18: Giải phương trình log₃x + log₉x + log₈₁x = 7

A. x = 27   B. x = 81   C. x = 729    D. x = 243

Câu 19: Nếu (log₃x)(log_2xy) = log_xx² thì y bằng

A. 9   B. 9/2    C. 18   D. 81

Hướng dẫn giải và Đáp án

Câu 13:

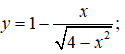
y’ = 0 => x = √2; y(√2) = 2√2

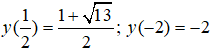
Câu 15:

log₃5. log₄9. log₅2 = (log₃5.log₅2).log_2²3² = log₃2.log₂3 = 1

Câu 16:

y’ = (√3)^x2.ln√3(x²)’

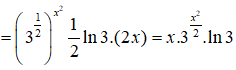
Câu 17:

4^x – 4^{x – 1} = 24 => 4^x – 4^x/4 = 24 => 3.4^x/4 = 24 => 2^2x = 32 = 2⁵ => 2x = 5

=> x = 5/2 => (2x)^x = 5^5/2 = 25√5

Câu 18:

log₃x + log₉x + log₈₁x = 7

<=> log₃x = 4 <=> x = 3⁴ = 81

Câu 19:

(log₃x)(log_x(2x))(log_2xy) = log_xx² <=> (log₃(2x))log_2xy = 2log_xx <=> log₃y = 2 <=> y = 3² = 9

Comments

comments