![[Giải Toán 10] Chương 1: Mệnh đề – Tập hợp/ Bài 3: Các phép toán tập hợp [Giải Toán 10] Chương 1: Mệnh đề – Tập hợp/ Bài 3: Các phép toán tập hợp](https://lop12.edu.vn/wp-content/uploads/2019/10/t3.png)
Trả lời câu hỏi Toán 10 Đại số Bài 3 trang 13: Cho
A = { n ∈ N | n là ước của 12}
B = { n ∈ N | n là ước của 18}
a)Liệt kê các phần tử của A và của B
b) Liệt kê các phần tử của tập hợp C các ước chung của 12 và 18
Lời giải
a) A = {1;2;3;4;6;12}
B = {1;2;3;6;9;18}
b) C = {1;2;3;6}
Trả lời câu hỏi Toán 10 Đại số Bài 3 trang 14: Giả sử A, B lần lượt là tập hợp các học sinh giỏi Toán, giỏi Văn của lớp 10E. Biết
A = { Minh, Nam, Lan, Hồng, Nguyệt };
B = { Cường, Lan, Dũng, Hồng, Tuyết, Lê };
(Các học sinh trong lớp không trùng tên nhau)
Gọi C là tập hợp đội tuyển thi học sinh giỏi của lớp gồm các bạn giỏi Toán hoặc giỏi Văn. Hãy xác định tập hợp C.
Lời giải
C={Minh, Nam, Lan, Hồng, Nguyệt; Cường, Dũng, Tuyết, Lê}
Trả lời câu hỏi Toán 10 Đại số Bài 3 trang 14: Giả sử tập hợp A các học sinh giỏi của lớp 10E là
A = { An, Minh, Bảo, Cường, Vinh, Hoa, Lan, Tuệ, Quý}.
Tập hợp B các học sinh của tổ 1 lớp 10E là
B = { An, Hùng, Tuấn, Vinh, Lê, Tâm, Tuệ, Quý}.
Xác định tập hợp C các học sinh giỏi của lớp 10E không thuộc tổ 1.
Lời giải
C = {Minh, Bảo, Cường, Hoa, Lan}
Bài 1 (trang 15 SGK Đại số 10): Kí hiệu A là tập hợp các chữ cái trong câu “CÓ CHÍ THÌ NÊN”, B là tập hợp các chữ cái trong câu “CÓ CÔNG MÀI SẮT CÓ NGÀY NÊN KIM”. Hãy xác định A ∩ B, A ∪ B, A \ B và B \ A.
Lời giải:
Ta có: A = {C, O, H, I, T, N, Ê }; B = {C, O, N, G, Ô, M, A, Ă, I, S, T, Y, Ê, K}
+ A ∩ B = {C, O, I, T, N, Ê}
+ A ∪ B = { C, O, Ô, N, G, M, A, Ă, I, S, T, Y, Ê, K, H}
+ A \ B = {H}
+ B \ A = {G, S, K, M, A, Ô, Ă, Y}
Kiến thức áp dụng
+ A ∩ B (A giao B) là tập hợp các phần tử chung của A và B.
A ∩ B = {x | x ∈ A và x ∈ B}.
+ A ∪ B (A hợp với B) là tập hợp các phần tử hoặc thuộc A hoặc thuộc B.
A ∪ B = {x | x ∈ A hoặc x ∈ B}.
+ A \ B (phần bù của B trong A) là tập hợp các phần tử thuộc tập A mà không thuộc tập B.
A \ B = { x | x ∈ A và x ∉ B}.
+ Tương tự B \ A (phần bù của A trong B) là tập hợp các phần tử thuộc tập hợp B mà không thuộc tập hợp A.
B\A = {x | x ∈ B và x ∉ A}.
Bài 2 (trang 15 SGK Đại số 10): Vẽ lại và gạch chéo các tập hợp A ∩ B , A ∪ B, A \ B (h.9) trong các trường hợp sau:
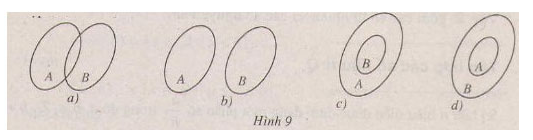
Lời giải:
a)
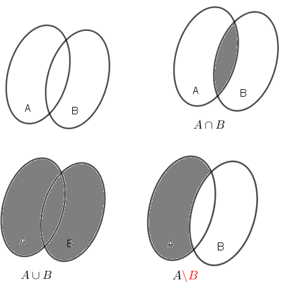
b)
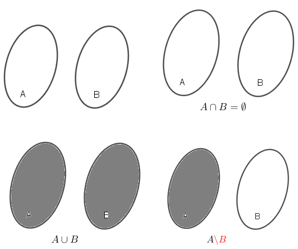
c)
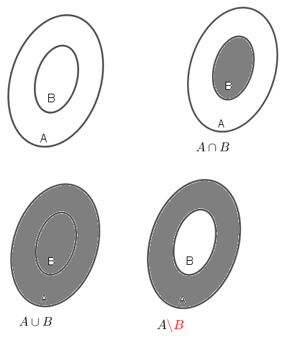
d)
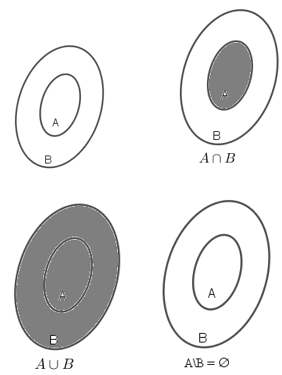
Kiến thức áp dụng
+ A ∩ B (A giao B) là tập hợp các phần tử chung của A và B.
A ∩ B = {x | x ∈ A và x ∈ B}.
+ A ∪ B (A hợp với B) là tập hợp các phần tử hoặc thuộc A hoặc thuộc B.
A ∪ B = {x | x ∈ A hoặc x ∈ B}.
+ A \ B (phần bù của B trong A) là tập hợp các phần tử thuộc tập A mà không thuộc tập B.
A \ B = { x | x ∈ A và x ∉ B}.
Bài 3 (trang 15 SGK Đại số 10): Trong số 45 học sinh của lớp 10A có 15 bạn được xếp loại học lực giỏi, 20 bạn được xếp loại hạnh kiểm tốt, trong đó có 10 bạn vừa học lực giỏi, vừa có hạnh kiểm tốt. Hỏi
a) Lớp 10A có bao nhiêu bạn được khen thưởng, biết rằng muốn được khen thưởng bạn đó phải học lực giỏi hoặc có hạnh kiểm tốt?
b) Lớp 10A có bao nhiêu bạn chưa được xếp loại học lực giỏi và chưa có hạnh kiểm tốt?
Lời giải:
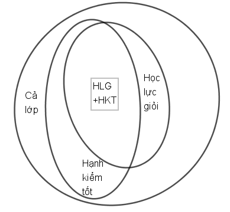
a) Các bạn được HLG = 15.
Các bạn được HKT = 20.
Số bạn HLT + HKT = 10.
⇒ Số bạn được HKT mà không được HLG = 20 – 10 = 10.
Số bạn được HLG mà không được HKT = 15 – 10 = 5.
Vậy số bạn được khen thưởng = (số bạn được HKT mà không được HLG)
+ (số bạn được HLG mà không được HKT)
+ (số bạn vừa được HLG, vừa được HKT)
= 5 + 10 + 10 = 25 (bạn).
b) Số học sinh chưa được xếp loại HLG và chưa có HKT là: 45 – 25 = 20 (bạn).
Bài 4 (trang 15 SGK Đại số 10): Cho tập hợp A, hãy xác định A ∩ A, A ∪ A, A ∩ ∅, A ∪ ∅, CAA, CA∅
Lời giải:
+ A ∩ A = A + A ∪ A = A
+ A ∩ ∅ = ∅ + A ∪ ∅ = A
+ CAA = A \ A = ∅ + CA∅ = A \ ∅ = A.
Kiến thức áp dụng
+ Nếu B ⊂ A thì A \ B được gọi là phần bù của B trong A. Kí hiệu CAB.