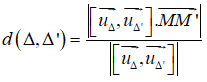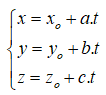
1. Phương trình tham số và phương trình chính tắc của đường thẳng
a) Cho đường thẳng Δ đi qua điểm M0(x0; y0; z0) và nhận vectơ uΔ→ = (a; b; c), với uΔ→ ≠ 0→, làm một vectơ chỉ phương. Phương trình tham số của Δ là:
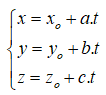
b) Nếu a, b, c đều khác 0 thì người ta còn viết phương trình của đường thẳng Δ dưới dạng chính tắc như sau:
![]()
2. Điều kiện để hai đường thẳng song song, trùng nhau, cắt nhau hoặc chéo nhau
Cho hai đường thẳng d và d’ lần lượt đi qua hai điểm M0(x0; y0; z0), M’0(x’0; y’0; z’0) và có vectơ chỉ phương lần lượt là:
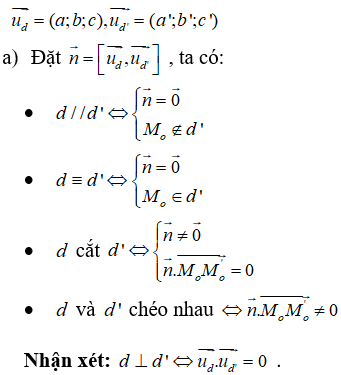
b) Xét hệ phương trình hai ẩn
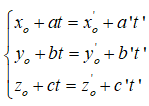
Khi đó:
– d và d’ cắt nhau khi và chỉ khi hệ (I) có đúng một nghiệm
– d và d’ chéo nhau khi và chỉ khi hai vectơ ud→, ud’→ không cùng phương và hệ (I) vô nghiệm.
3. Điều kiện để một đường thẳng song song, cắt hoặc vuông góc với mặt phẳng
Cho đường thẳng d đi qua điểm M0(x0; y0; z0) và có vectơ chỉ phương ud→ = (a; b; c) ; cho mặt phẳng (P) có phương trình là: Ax + By + Cz + D = 0. Gọi up→ = (A; B; C) là vectơ pháp tuyến của mặt phẳng (P). Ta có:
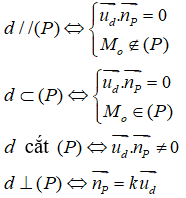
với k là một số thực nào đó.
4. Tính khoảng cách
a) Khoảng cách từ một điểm đến một đường thẳng
Trong không gian Oxyz, cho điểm A và đường thẳng Δ đi qua điểm M và có vectơ chỉ phương là uΔ→ = (a; b; c) . Để tính khoảng cách từ A đến đường thẳng Δ ta có hai cách:
Cách 1: Bước 1: Tìm hình chiếu vuông góc H của A trên đường thẳng Δ
Bước 2: Khoảng cách từ A đến đường thẳng Δ chính là khoảng cách giữa hai điểm A và H: d(A, Δ) = AH
Lưu ý: Để tìm được H ta có thể làm như sau: Viết phương trình tham số của đường thẳng Δ, từ đó suy ra tọa độ của điểm H dưới dạng tham số. Sau đó ta tìm được tọa độ H dựa vào điều kiện
![]()
Cách 2. Sử dụng công thức
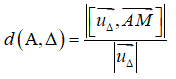
Hệ quả. Tính khoảng cách giữa hai đường thẳng song song
Cho hai đường thẳng song song Δ và Δ’. Gọi M, M’ lần lượt là một điểm tùy ý trên Δ và Δ’. Khi đó ta có: d(Δ, Δ’) = d(M, Δ’) = d(M’; Δ)
b) Khoảng cách giữa hai đường thẳng chéo nhau
Trong không gian Oxyz, cho hai đường thẳng chéo nhau Δ và Δ’, trong đó Δ đi qua điểm M và vectơ chỉ phương là uΔ→ = (a; b; c); Δ’ đi qua điểm M’ và vectơ chỉ phương uΔ’→ = (a’; b’; c’).
Để tính khoảng cách giữa hai đường thằng Δ và Δ’ ta có hai cách
– Cách 1.
Bước 1: Viết phương trình mặt phẳng (Q) chứa đường thẳng Δ’ và song song với Δ
Bước 2: Khoảng cách giữa hai đường thẳng Δ và Δ’ chính là khoảng cách giữa Δ và mặt phẳng (Q): d(Δ, Δ’) = d(Δ, (Q)) = d(M, (Q))
– Cách 2. Sử dụng công thức: