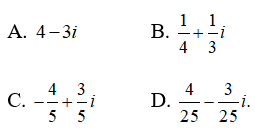
Câu 7: Cho các số phức z1 = 1 + i, z2 = 1 – i, z3 = 2 + 3i . Giá trị của biểu thức T = |z1z2 + z2z3 + z3z1| là
A. 6 B. 12 C. 6√2 D. 10.
Câu 8: Nghịch đảo của số phức z = 4 + 3i là
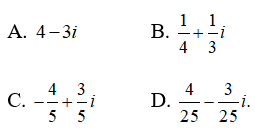
Câu 9:
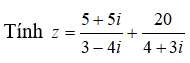
A. z = 3 – i B. z = 3 + i C. z = -3 + i D. z = -3 – i
Câu 10: Các số thực x, y thỏa mãn đẳng thức x(3 + 5i) – y(1 + 2i) = 9 + 16i . Giá trị biểu thức T = |x – y| là
A. 0 B. 1 C. 3 D. 5.
Câu 11: Cho số phức z thỏa mãn (1 + 2i)2.z + z− = 4i – 20. Môđun của z là
A. 4 B. 5 C. 6 D. 10
Câu 12: Phương trình z2 + az + b = 0 nhận z = 1 – 2i làm nghiệm. Khi đó a + b bằng
A. 3 B. 4 C. 5 D. 6.
Câu 13: Phương trình z2 + 1 = 2√2i có các nghiệm là z1, z2 . Tính T = |z1| + |z2|
A. 2 B. 2√2 C. 2√3 D. 12
Hướng dẫn giải và Đáp án
| 7-C | 8-D | 9-A | 10-D | 11-B | 12-A | 13-C |
Câu 7:
Ta có: z1z2 + z2z3 + z3z1 = z1z2 + z3(z1 + z2) = 1 – i2 + 2(2 + 3i) = 6 + 6i
Do đó: T = | z1z2 + z2z3 + z3z1 | = 6√2
Câu 8:
Nghịch đảo của số phức z = 4 + 3i là
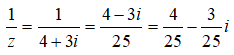
Câu 9:
Ta có
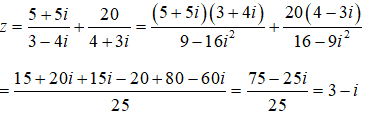
Câu 10:
Ta có: x(3 + 5i) – y(1 + 2i) = 9 + 16i <=> (3x – y) + (5x – 2y) = 9 + 16i
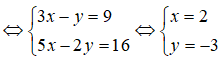
Vậy: T = |x – y| = 5
Câu 11:
Đặt a + bi(a, b ∈R). Ta có:
(1 + 2i)2z = (1 + 2i – 4)(a + bi) = -3a – 3bi + 4ai – 4b = -3a – 4b + (4a – 3b)i
Do đó: (1 + 2i)2.z + a− = 4i – 20 <=> -3a – 4b + (4a – 3b)i + a – bi = 4i – 20
<=> -2a – 4b + (4a – 4b)i = 4i – 20
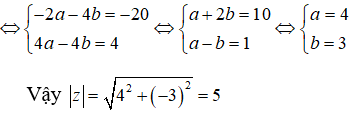
Câu 12:
Ta có z = 1 – 2i là nghiệm của phương trình đã cho nên:
(1 – 2i)2 + a(1 – 2i) + b = 0 <=> (a + b – 3) – (2a + 4)i = 0
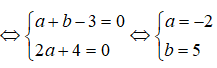
Vậy: a + b = -2 + 5 = 3
Câu 13:
Ta có: z2 = -1 + 2√2i = 1 + 2√2i + 2i2 = (1 + √2i)2 <=> z1,2 = ±(1 + √2i)
![]()
Chú ý. Có thể đặt z = a + bi(a,b ∈R). Ta có: z2 = a2 – b2 + 2abi. Từ giả thiết ta có :
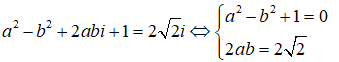
Từ đó suy ra a = 1, b = √2 hoặc a = -1, b = -√2
Do đó phương trình có hai nghiệm: z1,2 = ±(1 + *=√2i)