Chương 2 – Lý thuyết Bài 4: Hàm số mũ và hàm số lôgarit

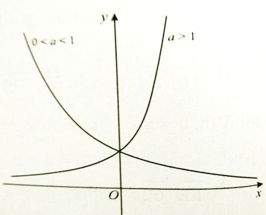
I. Hàm số mũ y = a^x (0 < a ≠ 1)

1. Tập xác định : R

2. Đạo hàm : y’ = (a^x)’ = a^xlna .

+ Đặc biệt (a^x)’ = e^x

3. Tính đơn điệu :

+ Nếu a > 1 thì hàm số đồng biến trên R

+ Nếu 0 < a < 1 thì hàm số nghịch biến trên R

4. Đồ thị :

+ Luôn cắt trục tung tại điểm (0 ;1)

+ Luôn nằm phía trên trục hoành

+ Nhận trục hoành làm tiệm cận ngang

II. Hàm số lôgarit y = log_ax (0 < a ≠ 1)

1. Tập xác định : D = (0; +∞)

2. Đạo hàm:

Đặc biệt: (lnx)’ = 1/x

3. Tính đơn điệu :

+ Nếu a > 1 thì hàm số đồng biến trên R

+ Nếu 0 < a < 1 thì hàm số nghịch biến trên R

4. Đồ thị :

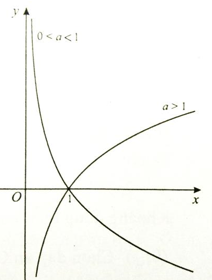
+ Luôn cắt trục hoành tại điểm (1 ;0)

+ Luôn nằm phía bên phải trục tung

+ Nhận trục tung làm tiệm cận đứng

Comments

comments