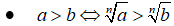
Xét hàm số lũy thừa y = xα, α ∈ R .
1. Tập xác định D của hàm số lũy thừa tùy thuộc vào giá trị của α . Cụ thể:
• Nếu α nguyên dương thì D = R ;
• Nếu α nguyên âm hoặc bằng 0 thì D = R\{0} ;
• Nếu α không nguyên thì D = (0; +∞) .
2. Đạo hàm: y’ = (xα)’ = α.xα – 1 (x > 0) .
3. Tính đơn điệu của hàm số lũy thừa( trên khoảng (0; +∞) ) tùy thuộc vào dấu của α . Cụ thể:
• Nếu α > 0 thì y đồng biến trên (0; +∞) .
• Nếu α < 0 thì y nghịch biến trên (0; +∞) .
Nhận xét: Từ đó ta thấy khi so sánh hai biểu thức lũy thừa cùng số mũ ( chẳng hạn aα và bα ) thì không nhưng ta cần so sánh giá trị của a và b mà còn phải xem xét đến dấu của α
Nói riêng, với nguyên dương, a, b > 0, ta có:
• a > b <=> an > bn
Đồ thị của hàm số lũy thừa
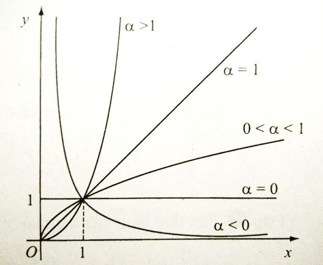
• Luôn đi qua điểm (1;1);
• Nếu α > 0 thì đồ thị không có tiệm cận;
• Nếu α < 0 thì đồ thị nhận trục hoành làm tiệm cận ngang, nhận trục tung làm tiệm cận đứng.
[…] sá» lÅ©y thừa nhÆ° khái niá»m, táºp xác Äá»nh, tÃnh Äá lop12.edu.vn Chương 2 – Lý thuyết Bài 2: Hàm số lũy thừa Xét hàm số lũy thừa y = xα, α ∈ […]
[…] sá» lÅ©y thừa nhÆ° khái niá»m, táºp xác Äá»nh, tÃnh Äá lop12.edu.vn Chương 2 – Lý thuyết Bài 2: Hàm số lũy thừa Xét hàm số lũy thừa y = xα, α ∈ […]
3working
gay phone chat line phone numbers https://gay-buddies.com/
liberty slots https://2-free-slots.com/
free double diamond slots https://freeonlneslotmachine.com/
las vegas slots free play https://candylandslotmachine.com/
free hot slots https://pennyslotmachines.org/
my konami slots https://slotmachinesworld.com/
youtube slots 2022 vegas https://slotmachinesforum.net/
yahoo slots farm https://beat-slot-machines.com/
slots capital https://download-slot-machines.com/
big fish free slots games https://411slotmachine.com/
cesars slots https://www-slotmachines.com/
casino joy slots https://slotmachinegameinfo.com/
dissertation help ireland statistics https://dissertations-writing.org/
dissertation service https://helpon-doctoral-dissertations.net/
Comments are closed.