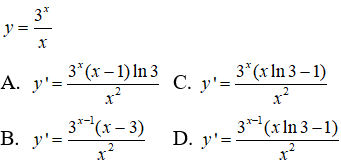
Câu 8: Giá trị của một chiếc xe ô tô sau t năm kể từ khi mua được ước lượng bằng công thức G(t) = 600e^-0,12t (triệu đồng). Tính giá trị của chiếc xe này tại hai thời điểm : lúc mua và lúc đã sử dụng 5 năm (làm tròn kết quả đến hàng triệu)

A. 532 và 329 (triệu đồng)    C. 600 và 292 (triệu đồng)

B. 532 và 292 (triệu đồng)    D. 600 và 329 (triệu đồng)

Câu 9: Tìm đạo hàm của hàm số y = x.2^3x

A. y’ = 2^3x(1 + 3xln2)    C. y’ = 2^3x(1 + 3ln3)

B. y’ = 2^3x(1 + xln2)    D. y’ = 2^3x(1 + xln3)

Câu 10: Tính đạo hàm của hàm số

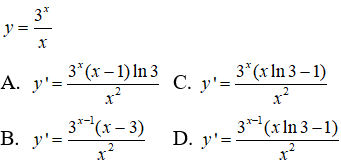
Câu 11: Tìm đạo hàm của hàm số

Câu 12: Viết phương trình tiếp tuyến của đồ thị hàm số y = xe^-2x + 2 tại giao điểm của đồ thị hàm số với trục tung

A. y = x + 2    B. y = x    C. y = 2x + 2    D. y = -2x + 2

Câu 13: Tìm các khoảng đồng biến của hàm số y = 4x – 5ln(x² + 1)

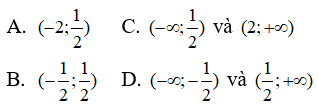
Câu 14: Cho hàm số y = x²e^-x . Khẳng định nào sau đây là đúng ?

A. Hàm số có x = 0 là điểm cực đại, x = 2 là điểm cực tiểu

B. Hàm số có x = 0 là điểm cực tiểu, x = -2 là điểm cực đại

C. Hàm số có x = 0 là điểm cực đại, x = -2 là điểm cực tiểu

D. Hàm số có x = 0 là điểm cực tiểu, x = 2 là điểm cực đại

Hướng dẫn giải và Đáp án

8-C

9-A

10-C

11-B

12-A

13-C

14-B

Câu 8:

Giá trị xe lúc mua: G(0) = 600 triệu đồng

Giá trị xe sau khi mua 5 năm : G(5) = 600.e^-0,12.5 ≈ 329 triệu đồng

Câu 9:

y’ = 2^3x + x.2^3x.ln(2)3 = 2^3x(1 + 3xln2)

Câu 10:

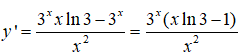
Câu 11:

Để thuận tiện, ta viết lại

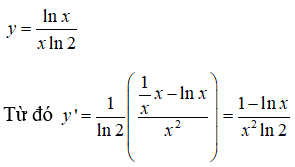
Câu 12:

y’ = e^-2x(1 – 2x); y'(0) = 1, y(0) = 2. Phương trình tiếp tuyến cần tìm : y = x + 2

Câu 13:

Tập xác định : R

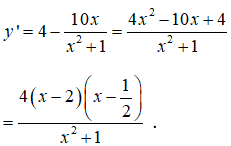
Bảng xét dấu

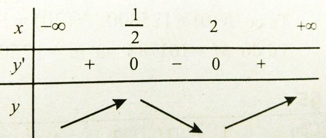
Khoảng đồng biến của hàm số là (-∞; 1/2) và (2; +∞)

Câu 14:

y’ = e^-xx(2 – x). Bảng biến thiên

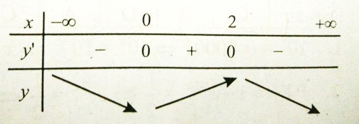
Từ bảng biến thiên ta thấy x = 0 là điểm cực tiểu, x = 2 là điểm cực đại của hàm số.

Comments

comments