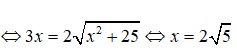
Câu 19: Trong các tiếp tuyến tại các điểm trên đồ thị hàm số y = x³ – 3x² + 2, tiếp tuyến có hệ số góc nhỏ nhất bằng:

A. -3   B. 3   C. -4   D. 0

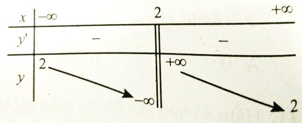
Câu 20: Hàm số nào sau đây có bảng biến thiên như hình bên?

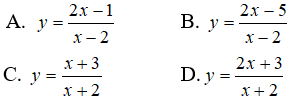
Câu 21: Hàm số y = x³ – 3x² + mx đạt cực tiểu tại x = 2 khi:

A.m < 0   B. m > 0    C. m = 0    D. m ≠ 0

Câu 22: Hàm số

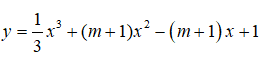
đồng biến trên tập xác định của nó khi:

A. -2 ≤ m ≤ -1    B. -2 < m < -1    C. m < -2   D. m > -1

Câu 23: Cho đồ thị hàm số y = x³ – 2x² + 2x (C). Gọi x₁,x₂ là hoành độ các điểm M, N trên (C), mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y = -x + 2017 . Khi đó (x₁, x₂) bằng

A. 4   B. -4/3    C. 4/3     D. -1

Câu 24: Một ngọn hải đăng đặt trại vị trí A cách bờbiển một khoảng AB = 5km. Trên bờ biển có một kho vị trí C cách B một khoảng là 7km. Do địa hình hiểm trở, người canh hải đăng chỉ có thể chèo thuyền từ A đến M trên bờ biển với vận tốc 4km/h rồi đi bộ đến C, với vận tốc 6km/h. Vậy vị trí M cách B một khoảng bao xa thì người đó đến kho là nhanh nhất?

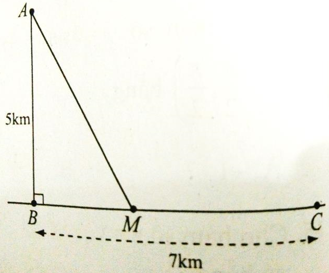
A. 3,5km   B. 4,5km   C. 5,5km   D. 6,5km

Hướng dẫn giải và Đáp án

Câu 19:

Tiếp tuyến của đồ thị hàm số có hệ số góc là

k = y’ = 3x² – 6x = 3(x – 1)² – 3 > -3 ∀x ∈ R

Câu 21:

Hàm số đạt cực tiểu tại x=2

Câu 23:

Tiếp tuyến của C vuông góc với đường thẳng y= -x + 2017 nên hệ số góc của tiếp tuyến là k₂ thỏa mãn (-1)k₂ = -1 => k₂ = 1

Suy ra k₂ = y’ = 1 => 3x² – 4x + 2 <=> 3x² – 4x + 2 = 0 (*)

Vì x₁, x₂ là nghiệm của (*) nên áp dụng Vi-ét ta có x₁ + x₂ = 4/3

Câu 24:

Đặt BM = x (0 ≤ x ≤ 7) => MC = 7 – x. Áp dụng định lí Py-ta-go cho tam giác vuông ABM có

Thời gian đi từ A đến M là

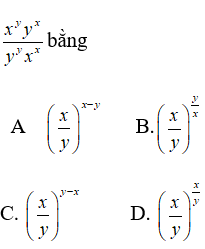
thời gian đi từ M đến C là

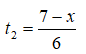
Tổng thời gian đi từ A đến C là

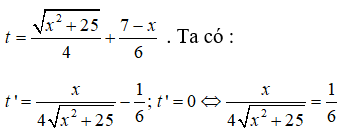
Bảng biến thiên

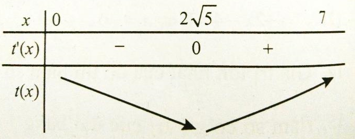
Để người đó đến kho nhanh nhất thì thời gian đi cần ít nhất, tức t đạt giá trị nhỏ nhất. Dựa vào bảng biến thiên ta thấy t đạt giá trị nhỏ nhất tại x = 2√5 ≈ 4,5

Vậy vị trí điểm M cách B một khoảng là 4,5km thì người đó đến kho là nhanh nhất.

Comments

comments