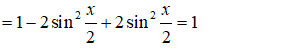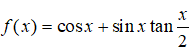
Câu 1: Cho hàm số y = – x3 + 3x2 – 3x + 1, mệnh đề nào sau đây là đúng?
A. Hàm số luôn nghịch biến.
B. Hàm số luôn đồng biến
C. Hàm số đạt cực đại tại x = 1
D. Hàm số đạt cực tiểu tại x = 1
Câu 2: Hàm số:
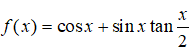
là hàm hằng trên khoảng nào sau đây?
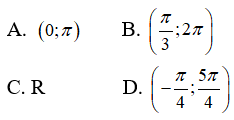
Câu 3: Cho hàm số y = x2 – 2|x| + 2 và các mệnh đề
(1) Hàm số trên liên tục trên R
(2) Hàm số trên có đạo hàm tại x = 0
(3) Hàm số trên đạt cực tiểu tại x = 0.
(4) Hàm số trên đạt cực đại tại x = 0.
(5) Hàm số trên là hàm chẵn
(6) Hàm số trên cắt trục hoành tại duy nhất một điểm
Trong các mệnh đề trên, số mệnh đề đúng là
A.1 B. 2 C.3 D. 4
Câu 4: Cho hàm số
![]()
và các mệnh đề sau
(1) Hàm số trên nhận điểm I(1;-1) làm tâm đối xứng,
(2) Hàm số trên nhận đường thẳng y = -x làm trục đối xứng.
(3) Hàm số trên nhận y = -1 là tiệm cận đứng.
(4) Hàm số trên luôn đồng biến trên R .
Trong số các mệnh đề trên, số mệnh đề sai là
A. 1 B.2 C.3 D. 4
Câu 5: Trong các khẳng định sau về hàm số
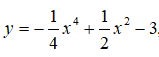
khẳng định nào là đúng?
A. Hàm số có điểm cực tiểu là x = 0
B. Hàm số có hai điểm cực đại là x = ±1
C. Cả A và B đều đúng;
D. Cả A và B đều sai,
Câu 6: Trong các mệnh đề sau, hãy tìm mện đề sai:
A. Hàm số y = -x3 + 3x2 – 3 có cực đại và cực tiểu;
B. Hàm số y = x3 + 3x + 1 có cực trị;
C. Hàm số
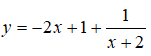
không có cực trị;
D. Hàm số
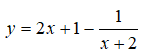
đồng biến trên từng khoảng xác định.
Hướng dẫn giải và Đáp án
| 1-A | 2-A | 3-C | 4-B | 5-C | 6-B |
Câu 1:
y’ = -3x2 + 6x – 3 = -3(x – 1)2 ≤ 0 ∀x ∈ R. Hàm số luôn nghịch biến.
Câu 2:
Điều kiện cos(x/2) ≠ 0 <=> x ≠ π + 2kπ (k ∈ Z)
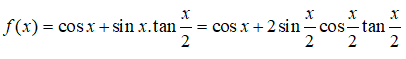
Hàm số là hàm hằng x ≠ π +2kπ (k ∈ Z)
Câu 3:
Mệnh đề 1, 4, 5 đúng. Mệnh đề 2, 3, 6 sai.
Câu 4:
+ Hàm số có tiệm cận đứng x=1 và tiệm cận ngang y=-1 Mệnh đề 1 đúng, mệnh đề 3 sai.
+ Vì đường thẳng y=-x là một phân giác của góc tạo bởi 2 đường tiệm cận nên đường thẳng y=-x là một trục đối xứng của đồ thị hàm số. Mệnh đề 2 đúng.
+ Hàm số có tập xác định là R\{1}, nên hàm số không thể luôn đồng biến trên R.Mệnh đề 4 sai.