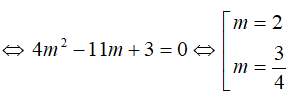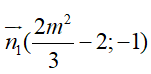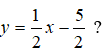
Câu 13: Với giá trị nào của m, đồ thị hàm số y = x3 – 3mx2 + m có hai điểm cực trị B, C thẳng hàng với điểm A(-1;3)?
A. m = 0 B. m = 1 C. m = -3/2 D. m = -3/2 hoặc m = 1
Câu 14: Cho hàm số y = x3 – 3x2 – 6x + 8 (C). Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số (C) là:
A. y = 6x – 6 B. y = -6x – 6 C. y = 6x + 6 D. y = -6x + 6
Câu 15: Cho hàm số y = x3 -3x2 – 9x + 4. Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số trên là:
A. y = -8x – 17 B. y = x + 7 C. y = -x + 1 D. Không tồn tại
Câu 16: Với giá trị nào của m, đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = x3 – 3x2 + 3mx + 1 – m tạo với đường thẳng Δ: 3x + y – 8 = 0 một góc 45o ?
A. m = 0 B. m = 2 C.m = 3/4 D. m = 2 hoặc m = 3/4
Câu 17: Với giá trị nào của m, đồ thị hàm số y = x3 + 3x2 + m2x + m có hai điểm cực trị đối xứng qua đường thẳng:
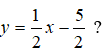
A. m = 0 B. m = 1 C. m = -1 D. Không tồn tại
Câu 18: Với giá trị nào của m, đồ thị hàm số y = x4 – 2mx2 + m 4 + 2m có ba điểm cực trị tạo thành tam giác đều?
A. m = 0 B. m = ∛3 C.-∛3 D. Không tồn tại
Hướng dẫn giải và Đáp án
| 13-D | 14-D | 15-A | 16-C | 17-D | 18-B |
Câu 13:
y’=3x2-6mx=3x(x – 2m)
Hàm số có hai điểm cực trị => y’=0 có hai nghiệm phân biệt <=> m ≠ 0 (*)
Tọa độ hai điểm cực trị là B(0;m) và C(2m;-4m3 + m)
AB→ =(1;m – 3); AC→ =(2m+1; -4m3 + m-3)
A, B, C thẳng hàng
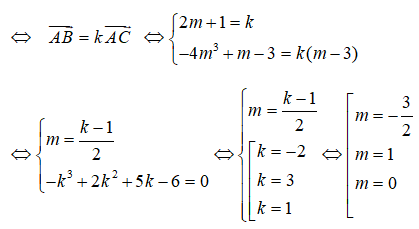
Đối chiếu với điều kiện (*) có m ∈ {-3/2; 1}
Câu 14:
Cách 1: Ta có y’=3x2-6x-6 ; y”=6x – 6
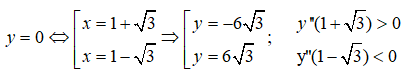
Do đó đồ thị hàm số có điểm cực trị là A(1 + √3; -6√3) và B(1 – √3; 6√3) .
Phương trình đường thẳng đi qua hai điểm cực trị là:
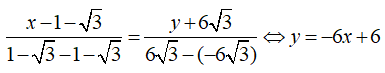
Cách 2: Ta có:
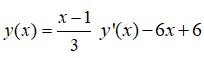
Gọi x1, x2 là nghiệm của phương trình y’(x)= 3x2-6x-6=0 . Khi đó ta có A(x1, y(x1)), BA(x2, y(x2)) là hai cực trị của đồ thị hàm số C với y'(x1) = y'(x2) = 0 .
Do đó ta có:
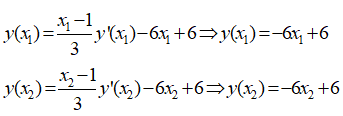
Vậy A, B thuộc đường thẳng y= – 6x+6.
Câu 15:
y’ = 3x2 – 6x – 9, y” = 6x – 6
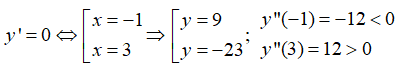
Do đồ thị hàm số có hai điểm cực trị là A(-1;0) và B(3;-23).
Phương trình đường thẳng đi qua hai điểm cực trị là:
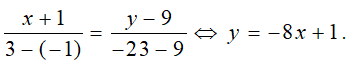
Câu 16:
Ta có y’ = 3x2 – 6x + 3m. Hàm số có hai điểm cực trị <=> y’=0 có hai nghiệm phân biệt
<=> Δ’ = 32 -3.3m > 0 <=> m < 1 (*)
Chia y cho y’ ta được:
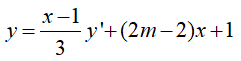
Giả sử x1, x2 là hai nghiệm phân biệt của y’=0
Phương trình đường thẳng đi qua hai điểm cực trị có dạng (d) : y= (2m-2)x+1
(d) có vectơ pháp tuyến là n1→ = (2m – 2; -1)
(Δ) : 3x+y-8=0 có vectơ pháp tuyến là n2→(3; 1)
Vì góc giữa đường thẳng (d) và (Δ) là 45o nên
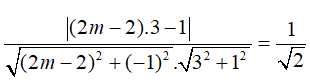
Đối chiếu điều kiện (*) có m = 3/4
Câu 17:
y’ = 3x2 + 6x + m2 . Hàm số có hai điểm cực trị => y’=0 có hai nghiệm phân biệt <=> Δ’ = 32 – 3.m2 > 0 <=> -√3 < m < √3
Chia y cho y’ ta được:
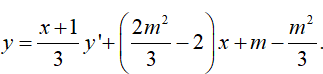
Giả sử x1, x2 là hai nghiệm phân biệt của y’=0.
Phương trình đường thẳng đi qua hai điểm cực trị có dạng
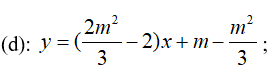
(d) có vectơ pháp tuyến là
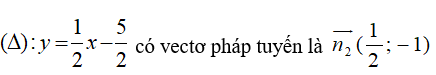
Vì hai điểm cực trị đối xứng với nhau qua (Δ) nên (d) ⊥ (Δ)
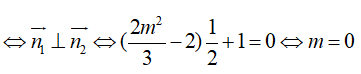
Thử lại khi m=0 ta có: y = x3 + 3x2; y’ = 3x2 + 6x; y” = 6x + 6
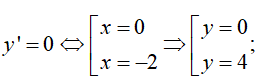
y”(0) = 6 > 0; y”(-2) = -6 < 0
Tọa độ hai điểm cực trị của đồ thị hàm số là O(0;0), A(-2;4)
Trung điểm của OA là I(-1;2).
Ta thấy I(-1,2) không thuộc đường thẳng (Δ) . Vậy không tồn tại m.
Câu 18:
y’ = 4x3 – 4mx = 4x(x2 – m)
Hàm số có ba điểm cực trị => y’=0 có ba nghiệm phân biệt <=> m > 0.
Khi đó đồ thị hàm số có ba điểm cực trị là :
A(0; m4 + 2m), B(-√m; m4 – m2 + 2m), C(√m; m4 – m2 + 2m)
ΔABC đều khi AB=AC
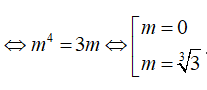
Đối chiếu với điều kiện tồn tại cực trị ta có m = ∛3 là giá trị cần tìm.