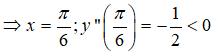
Câu 6: Cho hàm số y = x3 – 2x2 + 3. Điểm M(0; 3) là:
A. Cực đại của hàm số C. Điểm cực đại của đồ thị hàm số
B. Điểm cực đại của hàm số D. Điểm cực tiểu của đồ thị hàm số
Câu 7: Tìm điểm cực đại của hàm số y = sin2x + √3cosx + 1 với x ∈ (0; π)
A. x = 0 B. x = π C. π/6 D. π/3
Câu 8: Có bao nhiêu mệnh đề đúng trong các phát biểu sau?
1. Hàm số không có đạo hàm tại x = 0.
2. Hàm số không lien tục tại x = 0.
3. Hàm số không có cực trị tại x = 0.
4. Hàm số đạt cực trị tại x = 0.
A. 0 B. 1 C. 2 D. 3.
Câu 9: Cho hàm số y = -3x4 – 2x3 + 3
Hàm số có
A. Một cực đại và hai cực tiểu
B. Một cực tiểu và hai cực đại
C. Một cực đại và không có cực tiểu
D. Một cực tiểu và một cực đại.
Câu 10: Đồ thị hàm số nào sau đây có ba điểm cực trị (a là tham số nhận giá trị âm)?
A. y = x4 – 2ax2 + 3 B. y = ax4 – 2x2 + 3
C. y = a2x4 – 2x2 + 3 D. y = x4 + 2x2 + 3a
Câu 11: Tìm m để đồ thị hàm số y = x4 – 2(m + 1)x2 + m 2 có ba điểm cực trị tạo thành ba đỉnh của một tam giác vuông
A. m = 0 B. m = -1
C. m = 0 hoặc m = -1 D. Không có đáp án
Hướng dẫn giải và Đáp án
| 6-C | 7-C | 8-C | 9-C | 10-C | 11-A |
Câu 6:
Chọn đáp án C.
Chú ý. Phân biệt các khái niệm: cực trị, điểm cực trị của hàm số, điểm cực trị của đồ thị hàm số.
Câu 7:
Ta có: y’ = 2sinxcosx – √3sinx, y” = 2cos2x – √3cosx.
Với x ∈ (0; π) thì y’ = 2sinxcosx – √3sinx = 0
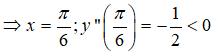
Nên hàm số đạt cực đại tại x = π/6 Chọn đáp án C.
Câu 8:
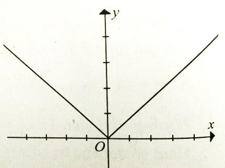
Đồ thị hàm số y = |x| có dạng hình vẽ.
Từ đồ thị trong hình ta có hàm số y = |x| liên tục tại x = 0 nhưng không có đạo hàm tại điểm đó. Sử dụng định nghĩa cực trị ta có hàm số y = |x| đạt cực tiểu tại x = 0
Do đó mệnh đề 1 và 4 đúng. Chọn đáp án C
Câu 9:
Ta có y’ = -12x3 – 4x
Xét y’=0 => x = 0
Hàm số chỉ có một cực đại tại x = 0. Chọn đáp án C.
Câu 10:
Để đồ thị hàm số có ba điểm cực trị thì y’ = 0 có ba nghiệm phân biệt. Do a là tham số nhận giá trị âm nên chỉ có y = a2x4 – 2x2 + 3 thỏa mãn. Chọn đáp án C
Câu 11:
Ta có: y’ = 4x3 – 4(m + 1)x = 4x(x2 – m – 1)
Để hàm số có ba điểm cực trị thì y’ = 0 có ba nghiệm phân biệt <=> m > – 1
Khi đó đồ thị hàm số có ba điểm cực trị là
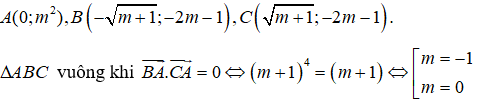
Đối chiếu điều kiện tồn tại cực trị ta có m = 0 là giá trị cần tìm. Chọn đáp án A.