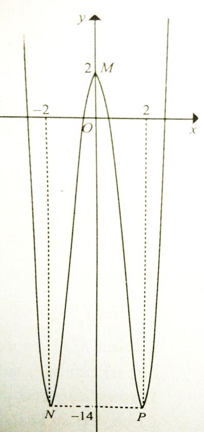
Câu 1: Cho hàm số y = f(x) có đồ thị như hình vẽ. Điểm cực đại của đồ thị hàm số là

A. M(0; 2) B. N(-2; -14)
C. P(2; -14) D. N(-2; -14) và P(2; -14)
Câu 2: Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên
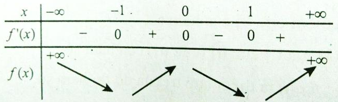
Mệnh đề nào sau đây là đúng?
A. Hàm số có đúng hai cực trị
B. Hàm số có điểm cực tiểu là -2
C. Hàm số có giá trị cực đại bằng 0.
D. Hàm số đạt cực đại tại x = 0 đạt cực tiểu tại x = -1 và x = 1
Câu 3: Tìm a, b, c sao cho hàm số y = x3 + ax2 + bx + c có giá trị bằng 0 khi x = 1 và đạt cực trị khi bằng 0 khi x = -1 .
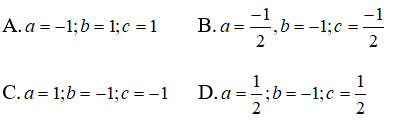
Câu 4: Trong các mệnh đề sau, mệnh đề nào đúng?
Nếu f'(x0) = 0 thì x0 là điểm cực trị của hàm số.
B. Nếu f'(x0) = 0 thì x0 là điểm cực đại của hàm số.
C. Nếu f'(x0) = 0 và f”(x0) > 0 thì x0 là điểm cực đại của hàm số.
D. Nếu f(x) có đạo hàm tại x0 và f’(x) đổi dấu khi x đi qua x0 thì x0 là điểm cực trị của hàm số.
Câu 5: Tìm tất cả các giá trị của tham số m để hàm số y = x3 – 2x2 +mx + 1 đạt cực đại tại x = 1.
A.m = -1 B. m = 1 C. m = 4/3 D. Không tồn tại.
Hướng dẫn giải và Đáp án
| 1-A | 2-D | 3-C | 4-D | 5-D |
Câu 1:
Dựa vào định nghĩa cực trị.
Chọn đáp án A.
Câu 2:
Dựa vào định nghĩa cực trị và bảng biến thiên.
Chọn đáp án D.
Câu 3:
Sử dụng giả thiết và điều kiện cần của cực trị ta có
y(1) = 0; y'(-1) = 0; y(-1) = 0
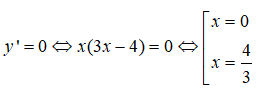
=> a = 1; b = -1; c = -1
Với a = 1; b = -1; c = -1 thì hàm số đã cho trở thành y = x3 + x2 – x – 1
Ta có y’ = 3x2 + 2x – 1, y” = 6x + 2. Vì y”=(-1) = -4 < 0 nên hàm số đạt cực đại tại x = -1 . Vậy a = 1; b = -1; c = -1 là các giá trị cần tìm.
Chọn đáp án C.
Câu 4:
Xem lại điều kiện cần và đủ để có cực trị của hàm số.
Chọn đáp án D.
Câu 5:
Ta có y’ = 3x2 – 4x + m
Hàm số đạt cực trị tại x = 1 thì y'(1) => m = 1
Với m = 1 thì hàm số đã cho trở thành y = x3 – 2x2 + x + 1
Ta có y’ = 3x2 – 4x + 1, y” = 6x – 4 Vì y”(1) = 2 > nên hàm số đạt cực tiểu tại x = 1.
Do vậy không có m thỏa mãn. Chọn đáp án D.
Chú ý. Sai lầm có thể gặp phải: khi giải y'(1) = 0 => m = 1 đã vội kết luận mà không kiểm tra lại, dẫn đến chọn đáp án B.