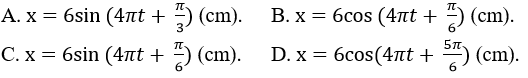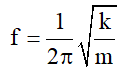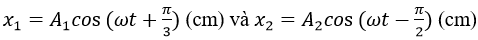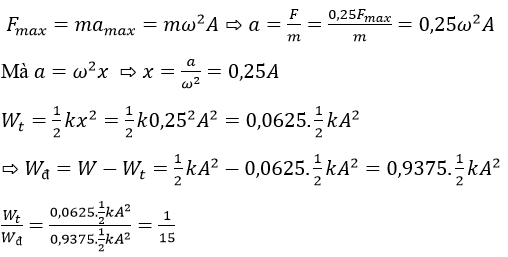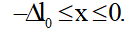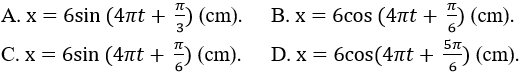
Câu 1: Một chất điểm dao động điều hòa trên đoạn thẳng MN dài 12 cm với tần số 2 Hz, Chọn gốc thời gian là lúc chất điểm có li độ 3√3 cm và chuyển động ngược chiều với chiều dương đã chọn. Phương trình dao động của chất điểm là

Câu 2: Một chất điểm dao động điều hòa với tấn số 3 Hz trên quỹ đạo là một đoạn thẳng dài 12 cm. Vận tốc của chất điểm có độ lớn cực đại bằng

A. 30 cm/s       B. 20 cm/s.       C. 113 cm/s       D. 0,52 m/s

Câu 3: Hai dao động điều hòa cùng phương, có các phương trình dao động là

Biên độ dao động tổng hợp là

A. 5√3 cm.       B. 2,5√3 cm.       C. 5 cm.       D. 2,5 cm.

Câu 4: Hai dao động điều hòa cùng phương, cùng tần số có các phương trình dao động là:

Phương trình dao động tổng hợp là: x=9cos⁡(ωt+ φ) (cm). Biên độ A₁ thay đổi được. Biết A₁ có giá trị sao cho A₂ có giá trị lớn nhất. Giá trị lớn nhất của A₂ khi đó là

A. 9 cm.       B. 18 cm.       C. 9√2 cm.       D. 9√3 cm.

Câu 5: Một vật dao động điều hòa theo phương ngang, mốc thế năng tại vị trí cân bằng. Khi lực tác dụng lên vật có giá trị bằng 0,25 độ lớn lực cực đại tác dụng lên vật thì tỉ số giữ thế năng và động năng của con lắc là

A. 16       B. 15       C. 1/15       D. 1/16

Câu 6: Một vật dao động điều hòa với chu kì bằng T, tại thời điểm t = 0 vật đi qua vị trí có li độ bằng một nửa biên độ và đang đi theo chiều âm của trục tọa độ. Trong thời gian 16T/3 kể từ t = 0 vật đi được quãng đường 1,29 m. Biên độ dao động của vật bằng

A. 6 cm       B. 8 cm       C. 10 cm       D. 5 cm

Câu 7: Một con lắc lò xo thẳng đứng, đầu dưới có vật m, dao động với biên độ 6,25 cm, tỉ số giữa lực cực đại và lực cực tiểu tác dụng vào điểm treo trong quá trình dao động là 5/3; lấy g = π² = 10 m/s². Tần số dao động là

A. 1 Hz       B. 0,5 Hz       C. 0,25 Hz       D. 0,75 Hz.

Hướng dẫn giải và đáp án

Câu	1	2	3	4	5	6	7
Đáp án	B	C	B	B	C	A	A

Câu 1: B

Phương trình dao động có dạng : x = Acos(ωt + φ)

⇒ Vận tốc v = – ωAsin(ωt + φ), trong đó A = 6 cm, ω = 2πf = 4π (rad/s).

Chọn gốc thời gian t = 0 là lúc x=3√3 cm , và v < 0

Câu 2: C

Vì chiều dài quỹ đạo L = 2A, nên biên độ dao động : A = 6 cm

|v_max |=Aω=6.2π.3=113 cm/s

Câu 3: B

A²=A₁²+A₂²+2A₁ A₂ cos(φ₁-φ² )=2A₁²+2A₂² cos π/3

⇒A=A₁ √3=2,5√3 cm

Câu 4: B

Ta có : A²=A₁²+A₂²+2A₁ A₂ cos(5π/6)

⟺A₁²-√3 A₂ A₁+A₂²-9²=0 (1)

Phương trình (1) có nghiệm A₁ khi Δ=3A₂²-4(A₂²-9² )≥0

⇒A₂≤18. Do đó A₂max=18 cm

Câu 5: C

Câu 6:

Câu 7: A

Comments

comments