Câu 19: Trong không gian Oxyz, cho hai điểm A(-1;0;2), B(1;-1;-2). Phương trình của mặt phẳng (P) đi qua A và vuông góc với đường thẳng AB là:
A. 2x – y – 4z + 10 = 0 C. x – y – 2z + 5 = 0
B. 2x – y – 4z – 10 = 0 D. 2x – y – 3z – 8 = 0
Câu 20: Trong không gian Oxyz, lập phương trình của mặt cầu (S) có bán kính bằng 5 và tiếp xúc với mặt phẳng (P): 3x – 4y – 4 = 0 tại điểm A(4;2;1)
A. (x – 7)2 + (y + 2)2 + (z – 1)2 = 25
B. (x – 7)2 + (y + 2)2 + (z – 1)2 hoặc (x – 1)2 + (y – 6)2 + (z – 1)2 = 25
C. (x + 7)2 + (y – 2)2 + (z + 1)2 = 25
D. (x + 7)2 + (y – 2)2 + (z + 1)2 hoặc (x + 1)2 + (y + 6)2 + (z + 1)2 = 25
Câu 21: Vị trí tương đối của hai đường thẳng
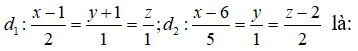
A. Cắt nhau B. song song C. chéo nhau D. trùng nhau
Câu 22: Trong không gian Oxyz, tọa độ điểm N đối xứng với điểm M(-5 ;2 ;-3) qua mặt phẳng (P) : 2x – 2y + z – 1 = 0 là :
A. N(3 ;-6 ;1) C. N(3 ;-2 ;-5)
B. N(-13 ;14 ;-7) D. Đáp án khác
Câu 23: Trong không gian Oxyz, cho ba điểm A(0 ;2 ;-4), B(-3 ;5 ;2), C(6 ;-1 ;-1). Tìm tọa độ của điểm M thuộc mặt phẳng (Oxy) sao cho biểu thức MA2 + MB2 + MC2 đạt giá trị nhỏ nhất
A. (1;2;-1) B. (3;6;0) C. (1;2;0) D. (0;0;0)
Câu 24: Trong không gian Oxyz, cho mặt phẳng (P) đi qua điểm M(-1;-1;-1) và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C (khác O) sao cho O, A, B, C là bốn đỉnh của một hình chóp đều. Số mặt phẳng (P) thỏa mãn bài toán là:
A. 8 B. 6 C. 3 D. 4
Câu 25: Trong không gian Oxyz, cho bốn điểm A(3;4;0), B(1;2;0), C(2;0;1), D(-1;1;3). Hỏi có bao nhiêu mặt phẳng (P) đi qua A đồng thời (P) cách đều ba điểm B, C, D?
A. 0 B. 4 C. 1 D. Vô số
Hướng dẫn giải và Đáp án
| 19-A | 20-B | 21-A | 22-A | 23-C | 24-D | 25-B |