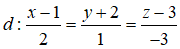
Câu 24: Trong không gian Oxyz, cho tứ diện ABCD với A(2;-4;6) và ba điểm B, C, D cùng thuộc mặt phẳng (Oyz). Gọi M, N, P lần lượt là trung điểm của AB, AC, AD. Lập phương trình mặt phẳng (MNP)
A. x + 1 = 0 C. y + z – 1 = 0
B. x – 1 = 0 D. x = 1 + t, y = -2, z = 3
Câu 25: Trong không gian Oxyz, cho đường thẳng d và mặt phẳng (P) lần lượt có phương trình là:
![]()
P): 2x + y – 3z – 4 = 0. Trong những khẳng định dưới đây, khẳng định nào đúng?
A. d nằm trong mặt phẳng (P) C. d không vuông góc với mặt phẳng (P)
B. d song song với mặt phẳng (P) D. d cắt mặt phẳng (P)
Câu 26: Trong không gian Oxyz, cho tứ diện ABCD với A(2;-4;6), B(1;1;1), C(0;3;0), D(0;0;3). Viết phương trình tham số của đường thẳng d chứa đường cao AH của tứ diện ABCD
A. x = 2 + t, y = -4 – t, z = 6 + t C. x = 2 + t, y = -4 + t, z = 6 + t
B. x = 1 + 2t, y = -1 -4t, z = 1 + 6t D. x = 1 + 2t, y = 1 – 4t, z = 1 + 6t
Câu 27: Trong không gian Oxyz, cho hai đường thẳng cắt nhau:d1: x = 1 + t, y = 1, z = 1 – t, d2: x = -t, y = 2 + t, z = 1. Viết phương trình của mặt phẳng (P) chứa hai đường thẳng d1, d2
A. x + y + z – 3 = 0 C. x – y + z – 1 = 0
B. x + y + z + 3 = 0 D. x – y + z + 1 = 0
Câu 28: Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là mx + y – 3z + 1 = 0; 4x – 2y + (n2 + n)z – n = 0, trong đó m và n là hai tham số. Với những giá trị nào của m và n thì hai mặt phẳng (P) và (Q) song song với nhau
A. m=-2 và n=2 C. m=-2 và n=2 hoặc n=-3
B. m=2 và n=-3 D. m=-2 và n=-3
Câu 29: Trong không gian Oxyz, cho đường thẳng
![]()
và mặt phẳng (P): 2x – y + 2z = 0. Cho mặt cầu (S) có tâm I thuộc đường thẳng d, có bán kính bằng 1 và tiếp xúc với mặt phẳng (P). Tọa độ tất cả các điểm I có thể là:
A. I1(5; 11; 2) C. I2(3; 7; 1) hoặc I3(-3; -5; -2)
B. I2(3; 7; 1) D. I1(5; 11; 2) hoặc I4(-1; -1; -1)
Câu 30: Trong không gian Oxyz, lập phương trình của mặt cầu (S) đi qua 3 điểm O, A(2;0;0), B(0;2;0) và tâm thuộc mặt phẳng (P): x + y + z – 3 = 0
A. (x – 1)2 + (y – 1)2 + (z – 1)2 = 3 C. (x – 1)2 + (y – 1)2 + (z – 1)2 = 9
B. (x + 1)2 + (y + 1)2 + (z + 1)2 = 3 D. (x + 1)2 + (y + 1)2 + (z + 1)2 = 9
Hướng dẫn giải và Đáp án
| 24-B | 25-D | 26-C | 27-A | 28-D | 29-D | 30-A |
Câu 25:
Ta có vectơ chỉ phương của đường thẳng d là : ud→ = (2; 1; -3), đồng thời nP→ = (2; 1; -3) = ud→ cũng là vectơ pháp tuyến của mặt phẳng (P). Do đó đường thẳng d vuông góc với mặt phẳng (P), suy ra đường thẳng d cắt mặt phẳng (P).
Câu 28:
Hai mặt phẳng đã cho song song khi và chỉ khi tồn tại một số thực k sao cho :
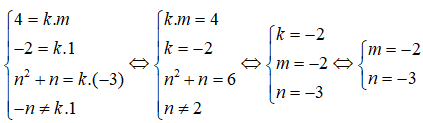
Câu 29:
Phương trình tham số của đường thẳng d là : d: x = 1 +2 t, y = 3+ 4t, z = t
Ta có I ∈ d => I(1 + 2t, 3 + 4t, t). Vì (S) tiếp xúc với mặt phẳng (P) nên ta có :
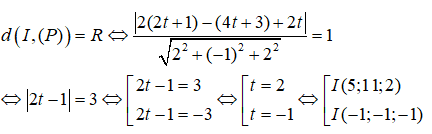
Câu 30:
Gọi I(a,b,c) là tâm của mặt cầu (S). Ta có:
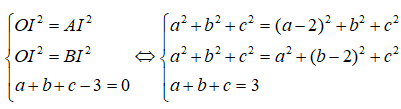
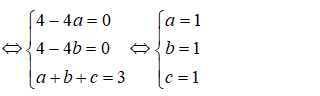
=> I(1; 1; 1); R = OI = √3
Vậy phương trình của mặt cầu (S) là: (x – 1)2 + (y – 1)2 + (z – 1)2 = 3