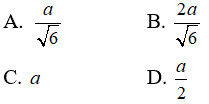
Câu 9: Cho hình chóp S.ABCD có SA ⊥ (ABCD) , đáy ABCD là hình chữ nhật. SA = 2AD = 2a . Góc giữa mp(SBC) và mặt đáy là 45^o . Gọi M là trung điểm của BC. Khoảng cách từ M đến mp(SBD) là:

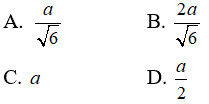
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của SA, SC. Biết thể tích của khối chóp S.BMN là a³ . Tính thể tích khối chóp S.ABCD

A. a³   B. 4a³   C. 8a³    D. 16a³

Câu 11: Cho hình chóp S.ABC có ∠ASB = ∠BSC = ∠CSA = 60^o, SA = 2SB = 3SC = 3a Thể tích khối chóp S.ABC là :

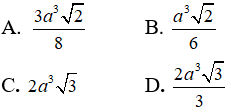
Câu 12: Cho hình chóp S.ABC có hình chiếu vuông góc của S lên mặt đáy là tâm O của đường tròn ngoại tiếp tam giác ABC. Biết SB = a và góc giữa cạnh bên SA và mặt đáy bằng 60^o . Diện tích của mặt cầu ngoại tiếp hình chóp S.ABC là :

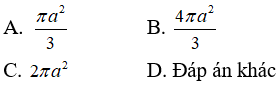
Câu 13: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA = AB = 2AD = 2a. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Bán kính của mặt cầu ngoại tâm B cắt SC theo một dây có độ dài 2a/3 là :

Câu 14: Hình nón có thiết diện cắt bởi mặt phẳng qua trục là một tam giác vuông và có diện tích xung quanh là √2 . Độ dài đường cao của hình nón là :

A. √2    B. 1   C. 1/√2    D. 2

Câu 15: Bạn Nam cao 1,8m tham gia trò chơi nhà bóng. Bạn Nam phải đứng thẳng trong quả bóng hình cầu và lăn trên cỏ. Để Nam có thể đứng được trong quả bóng thì Nam phải chọn quả bóng có thể tích ít nhất là bao nhiêu trong các kết quả sau:

A. π(m³)   B. 7,776π(m³)   C. 2,916π(m³)   D. 0,648π(m³)

Câu 16: Cho hình trụ có thể tích bằng 2π và có thiết diện cắt bởi mặt phẳng qua trục là hình vuông. Diện tích xung quanh của khối trụ là:

A. π   B. 2π   C. 4π/3   D. 4π

Hướng dẫn giải và Đáp án

9-A

10-C

11-A

12-B

13-C

14-B

15-A

16-D

Câu 9:

Từ giả thiết ta có :

=> AB = SA = 2a => V_S.BDM = (1/4)V_S.ABCD = a³/3

Mặt khác ta có :

SB = 2a√2; SD = a√5; BD = a√5 => S_ΔSBD = a²√6

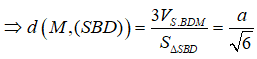
Câu 10:

Theo tỉ số thể tích ta có :

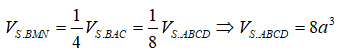
Câu 11:

Gọi A’,B’ lần lượt thuộc các cạnh SA, SB sao cho SA’ = SB’ = a. Khi đó SA’B’C’ là tứ diện đều cạnh bằng a. Theo công thức tỉ số thể tích ta có :

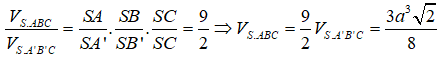
Câu 12:

Từ giả thiết ta có SO là trục của đường tròn ngoại tiếp tam giác ABC và SA=SB=a. Trong mặt phẳng (SAO), trung trực của cạnh SA cắt SO tại I thì I là tâm của mặt cầu ngoại tiếp hình chóp. Khi đó ta tính được :

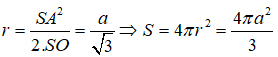
Câu 13:

Từ giả thiết ta có SA ⊥ (ABCD), theo định lí ba đường vuông góc ta có tam giác SBC vuông tại B. Gọi S(B,r) là mặt cầu tâm B cắt SC theo một dây có độ dài 2a/3. Khi đó ta tính được:

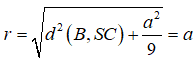
Câu 14:

Từ giả thiết ta có : 2α = 90^o => α = 45^o => h = r; l = r√2

Diện tích xung quanh của hình nón là : S_xq = πrl = πr²√2 = π√2 => r = 1 => h = 1

Câu 15:

Bạn Nam cao 1,8m nên đường kính của quả bóng không nhỏ hơn 1,8m hay bán kính không nhỏ hơn 0,9m. Do đó thể tích quả bóng thỏa mãn điều kiện là :

Câu 16:

Từ giả thiết ta có : h = 2r; V = πr²h = 2π => r = 1, h = 2 => S_xq = 2πrh = 4π

Comments

comments