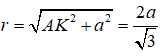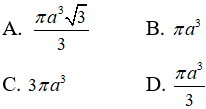
Câu 8: Cho khối trụ có diện tích toàn phần là 6πa2 và thể tích là 2πa3. Bán kính đáy của hình trụ là :
A. 3a/2 B. a C. 2a/3 D. 2a
Câu 9: Tam giác ABC vuông đỉnh A có ∠ ABC = 60o và AB = a. Quay miền trong và các cạnh của tam giác ABC quanh trục AB thì ta được khối nón (N). Thể tích của khối nón (N) là:
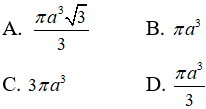
Câu 10: Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông cạnh a và cạnh bên bằng 2a. Thể tích khối nón có đỉnh là tâm O của hình vuông A’B’C’D’ và đáy là hình tròn ngoại tiếp hình vuông ABCD là :
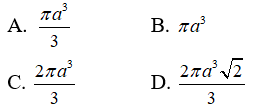
Câu 11: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Hai mặt phẳng (SAC) và (SAD) vuông góc với đáy. Khoảng cách từ A đến mặt phẳng (SBD) là a/2 . Bán kính mặt cầu tâm A cắt mặt phẳng (SBC) theo một đường tròn có bán kính bằng a là :
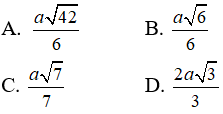
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với đáy và SA = 2a.Góc giữa cạnh bên SB và đáy là 45o . Bán kính mặt cầu tâm S và tiếp xúc với BD theo a là :
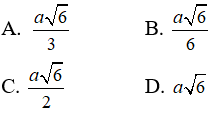
Câu 13: Cho hình chóp tứ giác đều S.ABCD có AB = a và góc giữa SA và đáy là 60o . Bán kính mặt cầu tâm A tiếp xúc với mặt phẳng (SBC) là :
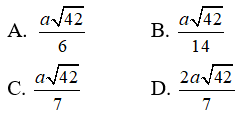
Câu 14: Cho hình chóp S.ABC có đáy ABC là tam giác vuông đỉnh A và BC = a. Cạnh bên SB vuông góc với mặt phẳng (ABC), SC tại với mặt phẳng (ABC) một góc là 60o. Bán kính mặt cầu ngoại tiếp hình chóp là :
A. a√3 B. a√2 C. a√3/2 D. a
Hướng dẫn giải và Đáp án
| 8-B | 9-B | 10-A | 11-D | 12-D | 13-C | 14-D |
Câu 8:
Từ giả thiết ta có:
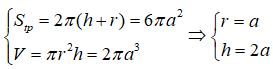
Câu 9:
Từ giả thiết ta có: h = AB = a; r = AC = atan60o = a√3 => (1/3).πr2h = πa3
Câu 10:
Từ giả thiết ta có: h = AA’ = 2a;
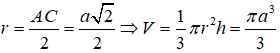
Câu 11:
Từ giả thiết ta có SA ⊥ (ABCD). Gọi O là tâm của hình vuông ABCD.
Hạ AH vuông góc với SA tại H. Khi đó ta chứng minh được AH là khoảng cách từ A đến mặt phẳng (SBD).
Khi đó xét tam giác vuông SAO ta có : SA = a√2/2 . Hạ AK vuông góc với SB tại K. Khi đó AK vuông góc với mặt phẳng (SBC) và AK = a/√3. Do đó ta có :