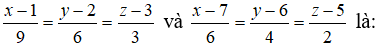
Câu 17: Vị trí tương đối của hai đường thẳng
![]()
A. Cắt nhau B. song song C. chéo nhau D. trùng nhau
Câu 18: Vị trí tương đối của hai đường thẳng
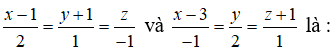
A. Cắt nhau B. song song C. chéo nhau D. trùng nhau
Câu 19: Vị trí tương đối của hai đường thẳng
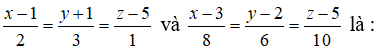
A. Cắt nhau B. song song C. chéo nhau D. trùng nhau
Câu 20: Tìm tất cả các giá trị của a để hai đường thẳng sau chéo nhau :
d1: x = 1 + at, y = t, z = -1 + 2t, d2: x = 1 – t’, y = 2 + 2t’, z = 3 – t’
A. a > 0 B. a ≠ -4/3 C. a ≠ 0 D. a = 0
Câu 21: Tìm tất cả các giá trị của a để hai đường thẳng sau vuông góc :
d1: x = 1 – t, y = 1 + 2t, z = 3 + at, d2: x = a + at, y = -1 + t, z = -2 + 2t
A. a=-2 B. a=2 C. a ≠ 2 D. Không tồn tại a
Câu 22: Vị trí tương đối của đường thẳng d: x = 1 + 2t, y = 1 – t, z = 1 – t và mặt phẳng (P): x + y + z – 3 = 0 là:
A. d ⊂ (P) B. cắt nhau C. song song D. Đáp án khác
Câu 23: Vị trí tương đối của đường thẳng d: x = 2 + 4t, y = 3 + t, z = -5t và mặt phẳng (P): x + y + z – 3 = 0 là :
A. d ⊂ (P) B. cắt nhau C. song song D. Đáp án khác
Câu 24: Vị trí tương đối của đường thẳng
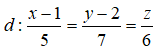
và mặt phẳng (P): x + y + z – 10 = 0 là :
A. d ⊂ (P) B. cắt nhau C. song song D. Đáp án khác
Hướng dẫn giải và Đáp án
| 17-D | 18-A | 19-C | 20-C | 21-A | 22-A | 23-C | 24-B |
Câu 17:
Do hai vectơ chỉ phương của hai đường thẳng đã cho cùng phương nên các đáp án A và C là sai. Trong hai đáp án còn lại, ta thấy điểm (1 ;2 ;3) thuộc đường thẳng còn lại. Vậy hai đường thẳng đã cho trùng nhau.
Câu 20:
Hai đường thẳng d1, d2 lần lượt đi qua hai điểm M1(1; 0; -1), M2(1; 2; 3) và có vectơ chỉ phương lần lượt là
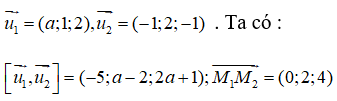
Hai đường thẳng chéo nhau khi và chỉ khi :
![]()
<=> -5.0 + (a – 2).2 + (2a + 1).4 ≠ 0 <=> 10a ≠ 0 <=> a ≠ 0
Câu 23:
Đường thẳng d đi qua điểm M(2 ;3 ;0) và có vectơ chỉ phương là ud→ = (4; 1; -5), mặt phẳng (P) có vectơ pháp tuyến là uP→ = (1; 1; 1). Ta có :
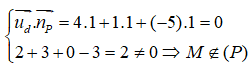
Suy ra đường thẳng d song song với mặt phẳng (P).