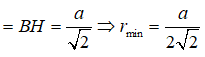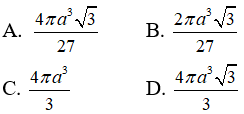
Câu 11: Cho hình chóp S.ABC có SA = SB = SC = a và tam giác ABC vuông tại A. Góc giữa SB với đáy là 60o . Thể tích khối cầu ngoại tiếp hình chóp là :
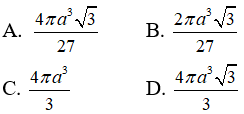
Câu 12: Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại A, BC = a√2 và góc giữa A’B và mặt phẳng (ABC) là 60o . Bán kính của mặt cầu ngoại tiếp lăng trụ là :
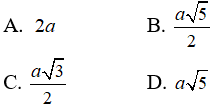
Câu 13: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 2a, ΔSAB là tam giác vuông cân đỉnh S và mặt phẳng (SAB) vuông góc với mặt phẳng đáy hình chóp. Bán kính mặt cầu ngoại tiếp hình chóp là :
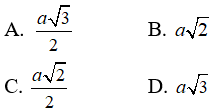
Câu 14: Cho hình nón có đường cao bằng đường kính đáy. Xét mặt cầu (S) nằm trong hình nón tiếp xúc với đáy và tất cả đường sinh của hình nón. Tỉ số thể tích của khối cầu và khối nón là :
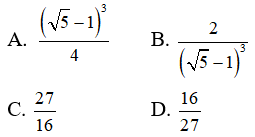
Câu 15: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân đỉnh A và AB = SB = a , SB vuông góc với mặt phẳng (ABC). Bán kính nhỏ nhất của mặt cầu tiếp xúc với đường thẳng SC và AB là :
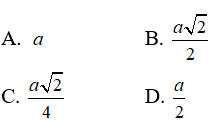
Hướng dẫn giải và Đáp án
| 11-A | 12-B | 13-B | 14-A | 15-C |
Câu 11:
Hạ SH ⊥ (ABC) tại H, khi đó ta có ΔSHA = ΔSHB = ΔSHC nên HA = HB = HC hay H là tâm đường tròn ngoại tiếp tam giác ABC. Ta có :
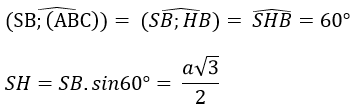
Trong mặt phẳng (SAH), đường trung trực của SA cắt SH tại I. Khi đó I cách đều các đỉnh của hình chóp nên I là tâm mặt cầu ngoại tiếp hình chóp. Gọi M là trung điểm của SA, khi đó ta có :
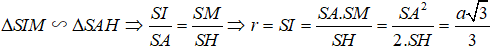
Khi đó thể tích khối cầu là :
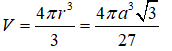
Câu 12:
Trong tam giác vuông ABC ta có
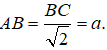
![]()
=> AA’ = AB.tan60o = a√3.
Gọi I là tâm của hình chữ nhật BCC’B’ và M là trung điểm của BC. Do tam giác ABC vuông tại A nên M là tâm đường tròn ngoại tiếp tam giác ABC và do đó IM là trục của đường tròn ngoại tiếp đáy ABC và I cách đều B, B’ nên I là tâm của mặt cầu ngoại tiếp lăng trụ. Khi đó ta có :
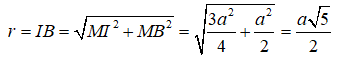
Câu 13:
Gọi H là trung điểm của AB, suy ra SH ⊥ AB. Khi đó ta có :
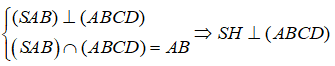
Gọi O là tâm của hình vuông ABCD. Xét tam giác vuông SAB có H là tâm đường tròn ngoại tiếp tam giác SAB. Khi đó ta có HO là trục của đường tròn ngoại tiếp tam giác SAB. Vậy điểm O cách đều các đỉnh của hình chóp và O là tâm mặt cầu ngoại tiếp hình chóp S.ABCD. Bán kính mặt cầu ngoại tiếp lăng trụ là :
r = OA = AC/2 = a√2
Câu 14:
GọiV1, V2 lần lượt là thể tích của khối cầu và khối nón. Từ giả thiết ta có h = 2r => l = r√5.
Gọi S, O lần lượt là đỉnh và tâm của hình nón. Gọi I là tâm của mặt cầu (S), khi đó I thuộc đoạn SO. Lấy một điểm A thuộc đường tròn đáy của hình nón. Gọi H là chân đường vuông góc hạ từ I lên SA, gọi r’ là bán kính của mặt cầu (S). Khi đó ta có IO = IH = r’
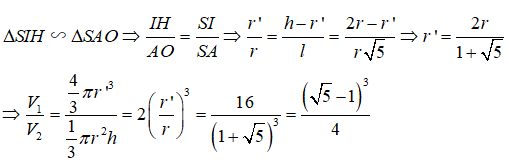
Câu 15:
Mặt cầu S(I,r) tiếp xúc với AB, SC lần lượt tại T, K. Khi đó ta có:
2r = IT + IK ≥ d(AB; SC) => r ≥ d(AB, SC)/2
Dựng hình bình hành ABDC, khi đó ta có ABDC là hình vuông cạnh a. Hạ BH vuông góc với SD tại H. Khi đó ta có BH ⊥ (SCD).
Suy ra: d(SC; AB) = d(AB, (SCD)) = d(B; (SCD))