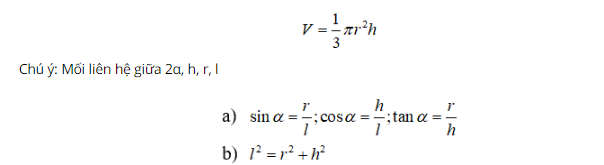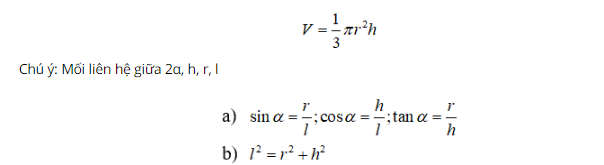
1. Sự tạo thành mặt tròn xoay
Trong không gian cho mặt phẳng (P) chứa đường thẳng Δ và chứ đường L. Khi quay mặt (P) xung quanh Δ một góc 360o thì đường L tạo nên một mặt tròn xoay. Mặt tròn xoay đó nhận Δ làm trục, đường L được gọi là đường sinh.
2. Tính chất của mặt tròn xoay
– Nếu cắt mặt tròn xoay bởi một mặt phẳng vuông góc với trục Δ ta được phần giao là đường tròn có tâm thuộc trục Δ
– Mỗi điểm M trên mặt tròn xoay đều nằm trên một đường tròn thuộc mặt tròn xoay và đường tròn này có tâm thuộc trục Δ
3. Mặt nón tròn xoay.
1. Định nghĩa.
Trong mặt phẳng (P) cho hai đường thẳng Δ và d cắt nhau tại điểm O và tạo với nhau một góc α với 0o < α < 90o. Mặt tròn xoay sinh ra bởi đường thẳng d khi quay mặt phẳng (P) xung quanh Δ gọi là mặt nón tròn xoay đỉnh O (được gọi tắt là mặt nón). Đường thẳng Δ được gọi là trục, đường thẳng d được gọi là đường sinh, góc 2α được gọi là góc ở đỉnh của mặt nón tròn xoay.
2. Tính chất
a) Nếu cắt mặt nón tròn xoay đỉnh O bởi mặt phẳng đi qua đỉnh O ta có các trường hợp sau đây:
– Mặt phẳng cắt mặt nón theo hai đường sinh
– Mặt phẳng tiếp xúc với mặt nón theo một đường sinh. Trong trường hợp này người ta thường gọi mặt phẳng đó là tiếp diện của mặt nón.
– Mặt phẳng chỉ có điểm O chung duy nhất với mặt nón, ngoài ra không có điểm chung nào khác.
b) Nếu cắt mặt nón tròn xoay đỉnh O bởi mặt phẳng (P) không đi qua đỉnh o ta có những trường hợp sau:
– Nếu mặt phẳng (P) cắt mọi đường sinh của mặt nón, ta được phàn giao là một đường elip hoặc một đường tròn (khi mặt phẳng (P) vuông góc với trục Δ của mặt nón)
– Nếu mặt phẳng (P) song song với chỉ một đường sinh của mặt nón ta được phần giao chính là một đường parabol
– Nếu mặt phẳng (P) song song với 2 đường sinh của mặt nón ta được phần giao là hai nhánh của một đường hypebol
3. Hình nón tròn xoay và khối nón tròn xoay
Cho tam giác OIM vuông tại I. Khi quay tam giác đó xung quanh cạnh góc vuông OI thì đường gấp khúc OMI tạo thành một hình được gọi là hình nón tròn xoay (hay được gọi tắt là hình nón). Hình tròn tâm I bán kính IM được gọi là mặt đáy, điểm O được gọi là đỉnh, độ dài đoạn OI gọi là chiều cao và độ dài đoạn OM được gọi là độ dài đường sinh của hình nón đó.
4. Diện tích xung quanh và diện tích toán phần của hình nón tròn xoay.
– Gọi Sxq là diện tích xung quanh của hình nón có bán kính đường tròn đáy bằng r và có độ dài đường sinh bằng l . Khi đó ta có công thức: Sxq = πrl
– Diện tích toàn phần của hình nón là tổng diện tích xung quanh và diện tích đáy. Gọi Stp là diện tích toàn phần của hình nón. Ta có công thức: Stp = πr(r + l)
5. Thể tích khối nón tròn xoay
Gọi V là thể tích khối nón tròn xoay có chiều cao h và có bán kính đáy r. Khi đó ta có công thức: