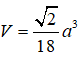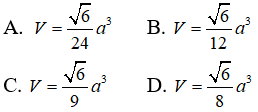
Câu 8: Tính thể tích V của hình chóp S.ABC có đáy là tam giác vuông tại A, SAB là tam giác đều cạnh a, mặt (SAB) vuông góc với đáy, BC = a√3
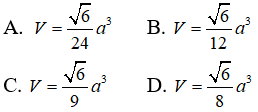
Câu 9: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M là trung điểm của SC, mặt phẳng qua AM và song song với BD cắt SB, SD lần lượt tại E, F. Tính tỉ số k giữa thể tích hình chóp S.AEMF và thể tích hình chóp S.ABCD.
A. k = 1/3 B. k = 1/4 C. k = 1/6 D. k = 1/9
Câu 10: Cho hình chóp S.ABC. Lấy các điểm A’, B’, C’ sao cho
![]()
Gọi V là thể tích hình chóp S.ABC, V’ là thể tích hình chóp S.A’B’C’.
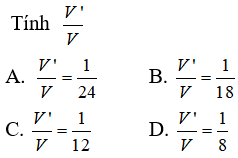
Câu 11: Cho hình chóp S.ABC có đáy là tam giác vuông cân ở B, AB = a, SA = a√2 và SA vuông góc với đáy. Gọi M, N lần lượt là chân đường cao hạ từ A đến SB và SC. Tính tỉ số k giữa thể tích hình chóp S.ANM và thể tích hình chóp S.ABC
A. k = 1/6 B. k = 1/4 C. k = 1/3 D. k = 1/2
Câu 12: Cho hình chóp S.ABC có đáy là tam giác vuông cân ở B, AB = a, SA = a√2 và SA vuông góc với đáy. Gọi M, N lần lượt là chân đường cao hạ từ A đến SB và SC. Tính thể tích V của hình chóp S.ANM
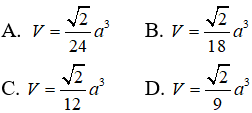
Câu 13: Tính thể tích hình chóp S.ABCD có đáy là hình chữ nhật, mặt SAB là tam giác đều, hình chiếu của S lên đáy trùng với trung điểm của AC, AC = 2a, AB = √3a
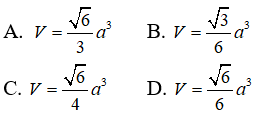
Câu 14: Cho hình chóp S.ABC có SC vuông góc với đáy, AB = a, AC = 2a, SC = BC = a√5. Mặt phẳng (P) qua C vuông góc với SB cắt SA, SB lần lượt tại A’, B’. Tính tỉ số k giữa thể tích hình chóp S.A’B’C’ và thể tích hình chóp S.ABC.
A. k = 5/18 B. k = 1/3 C. k = 7/18 D. k = 4/9
Hướng dẫn giải và Đáp án
| 8-B | 9-A | 10-A | 11-C | 12-B | 13-A | 14-A |
Câu 11:
Ta có: SN = SA√2/2 = a, SB = a√3
Dễ thấy CB ⊥ SB, AM ⊥ (SBC) suy ra SC ⊥ (ANM), do đó:
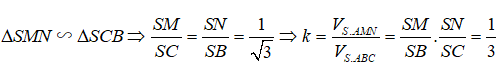
Câu 12:
Ta có:
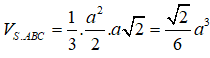
Áp dụng bài trên ta có: