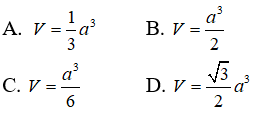
Câu 25: Tính thể tích V của hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a. Mặt bên tạo với đáy góc 45^o

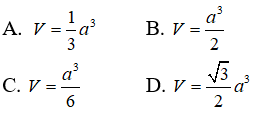
Câu 26: Tính thể tích V của hình chóp S.ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với đáy, cạnh bên SC tạo với mặt đáy góc 60^o

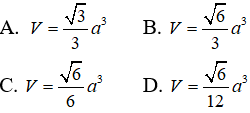
Câu 27: Tính thể tích V của hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, mặt bên (SDC) tạo với mặt đáy góc 60^o

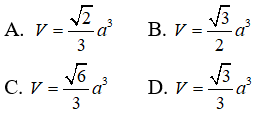
Câu 28: Tính thể tích V của hình chóp S.ABCD có đáy là hình vuông cạnh bằng a, SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBD) bằng √3a/3

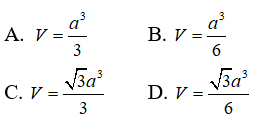
Câu 29: Tính thể tích V của hình chóp S.ABCD có đáy là hình bình hành, SAC là tam giác đều có cạnh bằng 2a, các mặt phẳng (SAC), (SBD) vuông góc với đáy, khoảng cách từ B đến mặt phẳng (SAC) bằng a√3/2

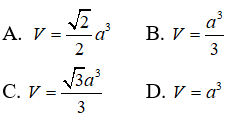
Câu 30: Tính thể tích V của hình chóp S.ABCD có đay là hình chữ nhật, SAB là tam giác đều có cạnh bằng 2a và thuộc mặt phẳng vuông góc với đáy, mặt bên (SDC) tạo với đáy một góc bằng 60^o

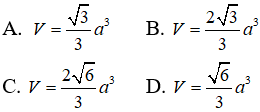
Câu 31: Tính thể tích V của hình chóp S.ABCD có đáy là hình thoi cạnh bằng a, góc ABC = 60^o , SA vuông góc với đáy và mặt bên (SBC) tạo với đáy một góc bằng 60^o .

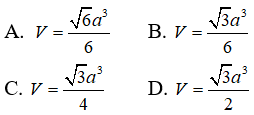
Câu 32: Tính thể tích V của hình chóp S.ABCD có đáy là hình thoi cạnh bằng a, góc ABC = 60^o , SA vuông góc với đáy, khoảng cách từ A đến mặt phẳng (SBD) bằng a√5/5

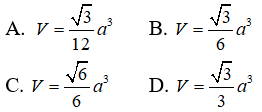
Câu 33: Tính thể tích V của hình chóp S.ABCD có đáy là hình thang vuông ở A và D. Hình chiếu của S lên đáy trùng với trung điểm của DC. Mặt (SBC) tạo với đáy một góc bằng 60^o, AB = AD = a, DC = 2a

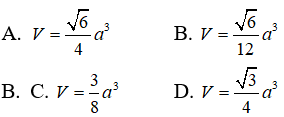
Hướng dẫn giải và Đáp án

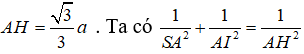
Từ đó tính được SA.

Câu 29:

V = 2V_B.SAC

Câu 30:

Gọi H, M lần lượt là trung điểm của AB và CD.

Khi đó SH là đường cao của hình chóp và góc tạo bởi mặt bên (SDC) với đáy bằng góc SMH

Câu 31:

Dễ thấy tam giác ABC đều. Gọi M là trung điểm của BC.

Khi đó góc SMA = 60^o, AM = a√3/3. Từ đó tính được SA.

Câu 32:

Dễ thấy tam giác ABC đều. Gọi I = AC ∩ BD kẻ AH ⊥ SI

Khi đó AH = a√5/5. Từ đó tính được SA.

Câu 33:

Gọi H, M lần lượt là trung điểm của DC và BC.

Khi đó SH là đường cao của hình chóp và góc SMH = 60^o. Từ đó tính được SH.

Comments

comments