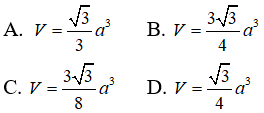
Câu 62: Cho hình lăng trụ ABC.A’B’C’ . Gọi E, F lần lượt là trung điểm của AA’, BB’. I là điểm tùy ý trên CC’. Tính thể tích V của hình chóp I.ABFE, biết thể tích của lăng trụ đã cho bằng 9.
A. V= 1/3 B. V= 3/2 C. V=3 D.V=6
Câu 63: Tính thể tích V của khối lăng trụ ABC.A’B’C’ , có cạnh bên bằng a, AB=AC=2a. (ABB’A’) ⊥ (ABC), góc BA’A = góc BAC = 90o
A. V = √3a3/2 B. V = √3a3 C. V = 2a3 D. V = 3a3
Câu 64: Cho hình lăng trụ ABC.A’B’C’ . Gọi E, F lần lượt là trung điểm của AA’, BB’. I là điểm tùy ý trên CC’. Gọi V’ là thể tích của hình chóp I.ABFE, V là thể tích của lăng trụ ABC.A’B’C’ . Tính tỉ số k = V’/V
A. k = 1/2 B. k = 1/3 C. k = 1/4 D. k = 1/6
Câu 65: Cho hình hộp BACD.A’B’C’D’ có đáy là hình thoi cạnh bằng a, góc BAD = 60o , hình chiếu của A’ lên mặt đáy trùng với trung điểm của AC, cạnh A’A tạo với đáy một góc 60o . Tính thể tích V của hình hộp đã cho
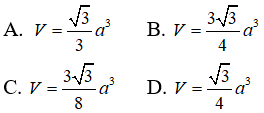
Câu 66: Tính tổng các khoảng cách h từ một điểm trong của một tứ diện đều cạnh a đến các mặt của nó.
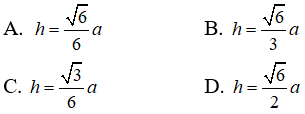
Câu 67: Cho hình lăng trụ đứng ABC.A’B’C’ , có AB = AC = 2, góc BAC = 120o . Biết thể tích của hình lăng trụ đã cho bằng √3a3 . Hãy tính góc α giữa hai mặt phẳng (ABC) và (A’BC)
A. α = 15o B. α = 30o C. α = 45o D. α = 60o
Câu 68: Cho hình lăng trụ đứng ABC.A’B’C’ ,có ABC = AC = 2a, góc BAC = 120o . Biết thể tích của hình lăng trụ đã cho bằng √3a3 . Hãy tính khoảng cách h từ B’ đến mặt (A’BC)
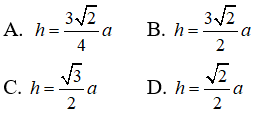
Câu 69: Cho hình lăng trụ tam giác đều ABC.A’B’C’ , có AB = 2, AA’ = 3. Lấy điểm E trên cạnh BB’ sao cho EB’=2EB. Mặt phẳng qua A’E, song song với BC cắt các đường thẳng CC’, AB, AC lần lượt tại F, M, N. Tính tỉ số k giữa thể tích hình lăng trụ ABC.A’B’C’ và thể tích hình chóp A’.AMN
A. k = 1/2 B. k = 2/3 C. k = 3/4 D. k = 4/3
Câu 70: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Gọi M, N lần lượt là trung điểm của các cạnh A’B’.C’D’ . Tính tỉ số k giữa thể tích của hình chóp D’.CNMP và thể tích hình lập phương ABCD.A’B’C’D’
A. k = 1/8 B. k = 1/6 C. k = 1/4 D. k = 1/3
Hướng dẫn giải và Đáp án
| 62-C | 63-B | 64-B | 65-B | 66-B | 67-C | 68-D | 69-D | 70-A |
Câu 62:
Gọi M là trung điểm của CC’. Ta có
Câu 64:
VI.ABFE = VC.ABFE = (2/3)VABC.EFM = (1/3)VABC.A’B’C’
Câu 68:
h = d(A, (A’BC))
Câu 69:
Để ý rằng:
2displays
i wanna fuck gay chat https://bjsgaychatroom.info/
free gay dating https://gaypridee.com/
gay video chat for windows 8 https://gaytgpost.com/
gay zoom chat rooms pnp https://gay-buddies.com/
military gay dating https://speedgaydate.com/
24 7 slots games https://candylandslotmachine.com/
best online slots https://pennyslotmachines.org/
free slots 777 sizzling 7s https://beat-slot-machines.com/
games slots https://download-slot-machines.com/
free slots black widow igt https://411slotmachine.com/
sharknado slots in vegas https://www-slotmachines.com/
ff7 cait sith slots limit https://slotmachinegameinfo.com/
professional dissertation writing https://buydissertationhelp.com/
masters dissertation help https://dissertationwriting-service.com/
writing an abstract for a dissertation https://help-with-dissertations.com/
dissertation improvement grant https://helpon-doctoral-dissertations.net/
Comments are closed.