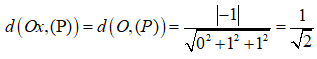
Câu 36: Trong không gian Oxyz, hai mặt phẳng 3x + 2y – mz + 2m – 7 = 0 và (5m + 1)x + (m + 3)y – 2z – 10 = 0. Trùng nhau khi và chỉ khi:
A. m = -4 C. m = 1
B. m = -6/5 D. Không có giá trị nào của m thỏa mãn
Câu 37: Trong không gian Oxyz, cho điểm A(1;2;-3) và mặt phẳng (P) có phương trình x – 2y + 2z + 1 = 0 . Khoảng cách từ A đến mặt phẳng (P) là:
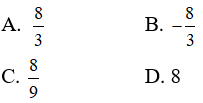
Câu 38: Trong không gian Oxyz, cho hai mặt phẳng song song (P): 4x – 3y – 8 = 0 và (Q): 8x – 6y – 1 = 0 . Khoảng cách giữa hai mặt phẳng (P) và (Q) là:
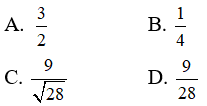
Câu 39: Trong không gian Oxyz, tập hợp các điểm M cách đều hai mặt phẳng tọa độ (Oxy) và (Oxz) là hai mặt phẳng có phương trình:
A. y+z=0 và y-z=0 C. x+z=0 và x-z=0
B. x+y=0 và x-y=0 D. y+2z=0 và y-2z=0
Câu 40: Trong không gian Oxyz, tập hợp các điểm cách đều hai mặt phẳng (P): x + 3y – 4z + 1 = 0 và (Q): x + 3y – 4z + 7 = 0 là :
A. x + 3y – 4z + 8 = 0 C. x + 3y – 4z + 4 = 0
B. x + 3y – 4z + 6 = 0 D. x + 3y – 4z – 6 = 0
Câu 41: Trong không gian Oxyz, tập hợp các điểm M cách đều hai mặt phẳng (P): 2x + 3y + z – 1 = 0 và (Q): 3x + y + 2z – 3 = 0 là hai mặt phẳng có phương trình là :
A. x – 2y + z – 2 = 0 và 5x + 4y + 4z – 4 = 0
B. x – 2y + z – 2 = 0 và 5x + 4y + 3z – 4 = 0
C. x – 3y + z – 2 = 0 và 5x + 4y + 3z – 4 = 0
D. x + 2y + z – 2 = 0 và 5x + 4y + 3z – 4 = 0
Câu 42: Trong không gian Oxyz, biết rằng trục Ox song song với mặt phẳng (P) : y + z – 1 = 0 . Khoảng cách giữa Ox và mặt phẳng (P) là :
Hướng dẫn giải và Đáp án
| 36-C | 37-A | 38-B | 39-A | 40-C | 41-B | 42-D |
Câu 36:
Hai mặt phẳng 3x + 2y – mz + 2m – 7 = 0 và (5m + 1)x + (m + 3)y – 2z – 10 = 0 trùng nhau khi và chỉ khi tồn tại một số thực k sao cho :
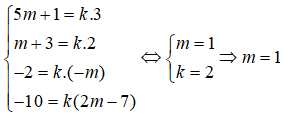
Câu 37:
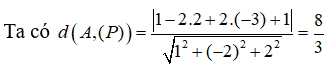
Câu 38:
Lấy một điểm M(2 ;0 ;0)∈(P). Vì hai mặt phẳng (P) và (Q) song song nên ta có :
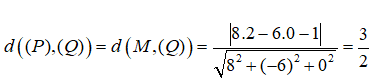
Câu 39:
Phương trình của hai mặt phẳng (Oxy) và (Oxz) lần lượt là z = 0 và y = 0.
Điểm M(x ;y ;z) cách đều hai mặt phẳng đó khi và chỉ khi
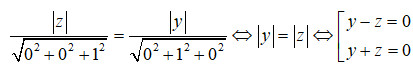
Câu 40:
Điểm M(x,y,z) cách đều hai mặt phẳng (P) và (Q) khi và chỉ khi
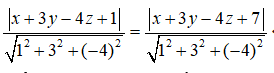
=> |x + 3y – 4z + 1| = |x + 3y – 4z + 7|
<=> x + 3y – 4z + 4 = 0
Câu 41:
Điểm M(x,y,z) cách đều hai mặt phẳng (P) và (Q) khi và chỉ khi :
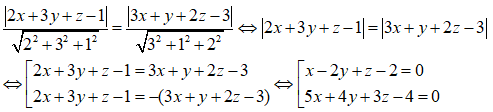
Câu 42:
Vì Ox song song với mặt phẳng (P) và O thuộc Ox nên ta có :