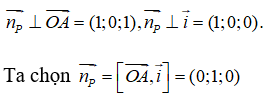
Câu 29: Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(1;0;1) và chứa trục Ox
A. x – 1 = 0 B. y = 0 C. z – 1 = 0 D. x + z – 1 = 0
Câu 30: Trong không gian Oxyz, cho mặt phẳng (P) có phương trình x + (m2 – 2m)y + (m – 1)z + m2 + m = 0 , trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) song song với trục Oy?
A. m=0 B. m=2 C. m=0 hoặc m=2 D. m=1
Câu 31: Trong không gian Oxyz, cho mặt phẳng (P) có phương trình 2x – 3y + (2m – 4)z + m2 – m = 0 , trong đó m là tham số. Với những giá trị nào của m thì (P) song song với trục Oz?
A. m=2 B. m=0 C. m=1 D. Không tồn tại m
Câu 32: Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là x + my + (m + 3)z + 1 = 0; x – y + 2z = 0 , trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) vuông góc với mặt phẳng (Q)?
A. m=-1 B. m=0 C. m=-7 D. Không tồn tại m
Câu 33: Trong không gian Oxyz, cho hai mặt phẳng (P) và (Q) lần lượt có phương trình là x – y + 2z = 0; 2x – 2y + (m2 + 3m)z + m2 – m = 0 , trong đó m là tham số. Với những giá trị nào của m thì hai mặt phẳng (P) và (Q) song song?
A. m=1 B. m=-4 C. m=1 hoặc m=-4 D. m=0
Câu 34: 34. Trong không gian Oxyz, cho ba mặt phẳng (P), (Q), (R) lần lượt có phương trình là (m2 + m)x – (m + 2)y + z = 0; x + y + z = 0; 2x + y – z = 0 và , trong đó m là tham số. Với những giá trị nào của m thì mặt phẳng (P) đồng thời vuông góc với cả hai mặt phẳng (Q) và (R)?
A. m=1 C. m= -3/2
B. m=-1 D. m= -3/2 hoặc m=-1
Câu 35: 35. Trong không gian Oxyz, cho hai mặt phẳng -mx + 3y + 2z + m – 6 = 0 và -2x + (5m + 1)y + (m + 3)z – 10 = 0. Hai mặt phẳng này cắt nhau khi và chỉ khi:
A. m ≠ -4 B. m ≠ -6/5 C. m ≠ 1 D. Mọi m
Hướng dẫn giải và Đáp án
| 29-B | 30-B | 31-A | 32-C | 33-B | 34-A | 35-C |
Câu 29:
Từ giả thiết suy ra
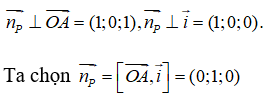
Từ đó suy ra phương trình của mặt phẳng (P) là : 1(y – 0) = 0 <=> y = 0
Câu 30:
Ta có np→ = (1; m2 – 2m; m – 1). Mặt phẳng (P) song song với trục Oy khi và chỉ khi
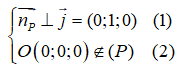
Ta có:
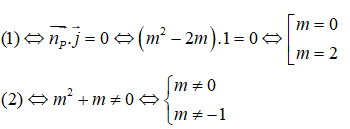
Từ đó ta được m=2. Vậy đáp án B là đúng
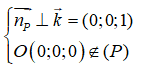
Câu 31:
Mặt phẳng (P) song song với trục Oz khi và chỉ khi
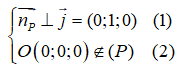
Câu 32:
Ta có: np→ = (1; m; m + 3), nQ→ = (1; -1; 2). Hai mặt phẳng (P) và (Q) vuông góc khi và chỉ khi np→.nQ→ = 0
<=> 1.1 + m.(-1) + (m + 3).2 = 0 <=> m + 7 = 0 <=> m = -7
Câu 33:
Hai mặt phẳng (P) và (Q) song song với nhau khi và chỉ khi tồn tại một số thực k sao cho
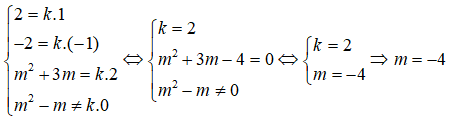
Câu 34:
Ta có:
![]()
Mặt phẳng (P) đồng thời vuông góc với cả hai mặt phẳng (Q) và (R) khi và chỉ khi
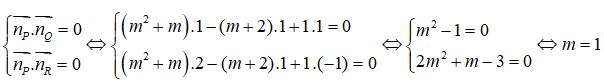
Câu 35:
Gọi hai mặt phẳng đã cho lần lượt là (P) và (Q). Ta có
![]()
Hai vectơ này song song khi và chỉ khi tồn tại một số thực k sao cho
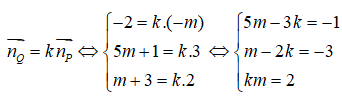
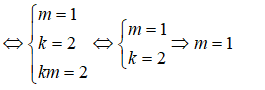
Từ đó suy ra hai mặt phẳng (P) và (Q) cắt nhau khi và chỉ khi hai vectơ pháp tuyến của chúng không song song, điều đó tương đương với m khác 1.