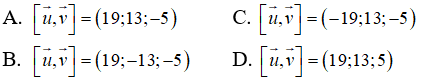
Câu 22: Trong không gian Oxyz, cho hai vectơ u→ = (-1; 3; 4), v→ = (2; -1; 5). Tích có hướng của hai vectơ u→ và v→ là:
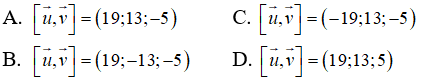
Câu 23: Trong không gian Oxyz, cho mặt phẳng (P) đi qua ba điểm A(1;1;1), B(2;3;-1), C(0;3;-2). Một vectơ pháp tuyến của mặt phẳng (P) là:
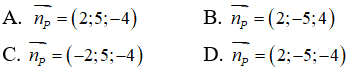
Câu 24: Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua ba điểm A(1;0;1), B(0;-1;-3), C(2;1;3)
A. x – y – 1 = 0 B. x – y + 1 = 0 C. x + z – 2 = 0 D. x + y – 1 = 0
Câu 25: Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm A(2;1;3), vuông góc với mặt phẳng (Q): x + y – 3z = 0 đồng thời (P) song song với trục Oz
A. x + y – 3 = 0 B. x – y – 1 = 0 C. 2x + y + 3z – 1 = 0 D. x – y + 1 = 0
Câu 26: Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm M(2;6;-3) và vuông góc với hai mặt phẳng (Oxy), (Oyz) là:
A. 2x – 4 = 0 B. y – 6 = 0 C. z + 3 = 0 D. 2x – 6y – 3z – 49 = 0
Câu 27: Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua điểm B(2;1;3) đồng thời vuông góc với hai mặt phẳng (Q): x + y – 3z = 0, (R): 2x – y – z = 0
A. 4x + 5y + 3z + 22 = 0 C. 2x + y + 3z – 22 = 0
B. 4x – 5y + 3z – 12 = 0 D. 4x + 5y + 3z – 22 = 0
Câu 28: Trong không gian Oxyz, lập phương trình của mặt phẳng (P) đi qua hai điểm A(1;0;1), B(2;1;3), đồng thời vuông góc với mặt phẳng (Q): x + y – 3z = 0
A. x – y – 1 = 0 B. x + y – 1 = 0 C. x + z – 1 = 0 D. x + y – 3z + 2 = 0
Hướng dẫn giải và Đáp án
| 22-A | 23-D | 24-A | 25-B | 26-B | 27-D | 28-A |
Câu 23:
Từ giả thiết ta suy ra
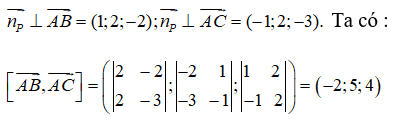
Từ đó suy ra np = (2; -5; -4)→ là một vectơ pháp tuyến của (P)
Câu 24:
Từ giả thiết ta suy ra:
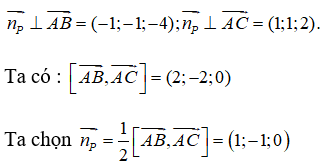
Từ đó suy ra phương trình của mặt phẳng (P) là : 1(x – 1) – 1(y – 0) = 0 <=> x – y – 1 = 0
Câu 25:
Từ giả thiết ta suy ra:
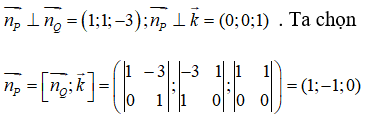
Mặt khác mặt phẳng (P) đi qua điểm A(2 ;1 ;3) nên ta có phương trình của mặt phẳng (P) là: 1(x- 2) – 1(y – 1) = 0 <=> x – y – 1 = 0
Câu 26:
Vì (P) vuông góc với hai mặt phẳng (Oxy), (Oyz) và (Oxy) (Oyz) = Oy nên ta có (P) → Oy => np→ = j→ = (0; 1; 0)
Từ đó suy ra phương trình của mặt phẳng (P) là : 0(x – 2) + 1(y – 6 ) + 0(z + 3) = 0 <=> y – 6 = 0
Câu 27:
Từ giả thiết suy ra:
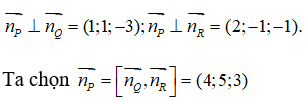
Mặt khác mặt phẳng (P) đi qua điểm B(2 ;1 ;3) nên ta có phương trình của mặt phẳng (P) là : 4(x – 2) + 5(y – 1) + 3(z – 3) = 0 <=> 4x + 5y + 3z – 22 = 0
Câu 28:
Từ giả thiết suy ra:
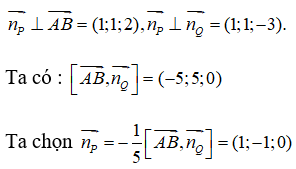
Từ đó suy ra phương trình của mặt phẳng (P) là : 1(x – 1) – 1(y – 0) = 0 <=> x – y – 1 = 0