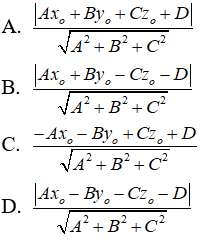
Câu 1: Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm M(x0, y0, z0) và có một vectơ pháp tuyến nP→ = (A; B; C) là:
A. Ax0 + By0 + Cz0 = 0
B. A(x + x0) + B(y + y0) + C(z + z0) = 0
C. A(x – x0) + B(y – y0) + C(z – z0) = 0
D. x0(x – A) + y0(y – B) + z0(z – C) = 0
Câu 2: Trong không gian Oxyz, phương trình của mặt phẳng (P) đi qua điểm M(-x0, y0, -z0) và có một vectơ pháp tuyến nP→ = (-A; B; -C) là:
A. A(x – x0) – B(y – y0) + C(z – z0) = 0
B. A(x + x0) – B(y – y0) + C(z + z0) = 0
C. A(x – x0) – B(y + y0) + C(z – z0) = 0
D. A(x + x0) – B(y + y0) + C(z + z0) = 0
Câu 3: Trong không gian Oxyz, cho điểm M(-x0; -y0; z0) và phương trình của mặt phẳng (P): Ax + By + Cz = D = 0 . Khoảng cách từ điểm M đến mặt phẳng (P) là:
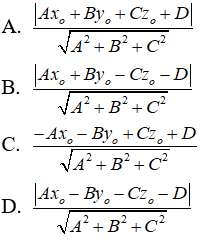
Câu 4: Trong không gian Oxyz, cho hai mặt phẳn song song (P): Ax + By + Cz + D = 0 và (Q): Ax + By + Cz + D’ = 0. M là một điểm di động trên mặt phẳng (P). Khẳng định nào dưới đây có thể sai?
A. Khoảng cách từ điểm M đến mặt phẳng (Q) không phụ thuộc vào M.
B. Khoảng cách giữa hai mặt phẳng (P) và (Q) chính là khoảng cách từ M đến mặt phẳng (Q)
C. Khoảng cách giữa hai mặt phẳng (P) và (Q) là
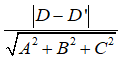
D. Khoảng cách giữa hai mặt phẳng (P) và (Q) là |D’ – D|
Câu 5: Trong các khẳng định dưới đây, khẳng định nào đúng?
A. Mỗi mặt phẳng chỉ có duy nhất một vectơ pháp tuyến
B. Mặt phẳng (P) hoàn toàn được xác định khi biết một điểm A thuộc (P) và biết một vectơ pháp tuyến của mặt phẳng (P)
C. Mặt phẳng (P) hoàn toàn được xác định khi biết một điểm A thuộc (P) và (P) vuông góc với một mặt phẳng (Q) cho trước
D. Mặt phẳng (P) hoàn toàn được xác định khi biết một điểm A thuộc (P) và (P) song song với một đường thẳng d cho trước
Câu 6: Trong các khẳng định dưới đây, khẳng định nào sai?
A. Phương trình của mặt phẳng (P) đi qua điểm M(x0; y0; z0) và có một vectơ pháp tuyến nP→ = (A; B; C) là: A(x – x0) + B(y – y0) + C(z – z0) = 0
B. Nếu hai mặt phẳng vuông góc với nhau thì hai vectơ pháp tuyến của chúng cũng vuông góc
C. Nếu hai mặt phẳng cắt nhau thì hai vectơ pháp tuyến của chúng không cùng phương
D. Nếu hai mặt phẳng (P) và (Q) có hai vectơ pháp tuyến cùng phương thì chúng song song
Câu 7: Trong không gian Oxyz, cho mặt phẳng (P) có phương trình là x – 2y + 2 = 0 . Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (P):
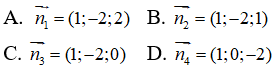
Hướng dẫn giải và Đáp án
| 1-C | 2-B | 3-B | 4-D | 5-B | 6-D | 7-C |