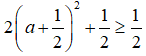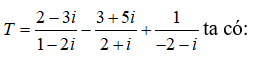
Câu 41: Thực hiện phép tính
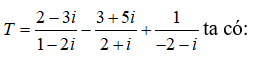
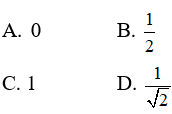
A. T = 1 + i B. T = 1 – i C. T = -1 + i D. T = -1 – i
Câu 42: Các số thực x, y thỏa mãn: (x + 2y) + (2x – y)i = 6 + 7i. Giá trị biểu thức T = x + y bằng:
A. 4 B. 5 C. 6 D. 7.
Câu 43: Phương trình z2 – 8z + 20 = 0 có hai nghiệm là
A. 8 ± 4i B. -8 ± 4i C. -4 ± 2i D. 4 ± 2i
Câu 44: Số phức z = a + bi có phần thực, phần ảo là các số nguyên và thỏa mãn: z3 = 2 + 11i. Giá trị biểu thức T = a + b là
A. 2 B. 3 C. 4 D. 5
Câu 45: Tập hợp các điểm biểu diễn số phức z thỏa mãn |i(z – 1) + 2| = |3 – 4i| là
A. Đường tròn tâm I(1; 2) bán kính R = 5
B. Đường tròn tâm I(1; -2) bán kính R = 5
C. Đường tròn tâm I(-1; 2) bán kính R = 5
D. Đường tròn tâm I(-1; -2) bán kính R = 5
Câu 46: Cho số phức z thỏa mãn |z− + 1 – i| = |z|. Giá trị nhỏ nhất của môđun của z là
Hướng dẫn giải và Đáp án
| 40-A | 41-D | 42-B | 43-D | 44-B | 45-A | 46-D |
Câu 41:
Ta có
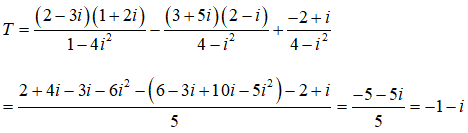
Câu 42:
Ta có: (x + 2y) + (2x – y)i = 6 + 7i
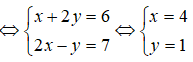
Vậy: T = 4 + 1 = 5
Câu 44:
Ta có: z3 = a3 + 3a2bi + 3ab2i2 + b3i3 = a3 – 3ab2 + (3a2b – b3)i
Từ giả thiết ta có:
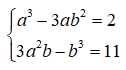
Từ phương trình thứ nhất ta có: a(a2 – 3b2). Vì a,b nguyên nên a là ước của 2.
Nếu a=1 thì 1 – 3b2 = 2. Suy ra b2 = -1/3 ∉ Z (loại)
Nếu a=-1 thì b = ±1 , không thỏa mãn phương trình thứ hai của hệ.
Nếu a=-2 thì b2 = 5/3 ∉ Z (loại).
Nếu a=2 thì b = ±1 . Kết hợp với phương trình thứ hai ta có: a = 2, b = 1
Vậy T = 3
Câu 45:
Đặt z = a + bi (a, b ∈ R). Ta có: i(z – 1) + 2 = i(a + bi – 1) + 2 = 2 – b + (a – b)i
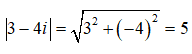
Do đó: |i(z – 1) + 2| = |3 – 4i| <=> (a – 1)2 + (b – 2)2 = 25
Tập hợp các điểm M(a,b) biểu diễn của số phức z là đường tròn tâm I(1;2), bán kính là R=5
Câu 46:
Cho số phức z thỏa mãn: |z− + 1 – i| = |z|
Đặt z = a + bi (a, b ∈ R) . Ta có: z− + 1 – i = a – bi + 1 – i = a + 1 – (b + 1)i
Từ giả thiết ta có : (a + 1)2 + (b + 1)2 = a2 + b2 <=> a + b + 1 = 0 <=> b = -1 -1
Khi đó |z|2 = a2 + b2 = a2 + ( -1 – a)2 = 2a2 + 2a + 1